写在前面
今次分享一下将正则化加入逻辑回归算法的实现
,其实也并不算复杂,所见即所得,所得就把它写出来。
正则化逻辑回归的实现
文件数据
在此次练习中用了一个更加复杂的数据集。与之前一样,我们需要先读数据,读完之后将它画出来看看分布。方法千千万,当然明显的是上一期的方法比较简便,不过选一种比较熟悉的就好。
with open(filename, 'r') as f:
reader = csv.reader(f)
columns = ['t1', 't2', 'value']
for row in reader:
save_list.append([float(row[0]), float(row[1]), int(row[2])])
df = pd.DataFrame(save_list, columns=columns)
画图方式与上一次的相同,使用matplotlib.pyplot就好
plt.plot(data_when_zero['t1'], data_when_zero['t2'], 'ro')
plt.plot(data_when_one['t1'], data_when_one['t2'], '+')
plt.xlabel('Microchip Test 1')
plt.ylabel('Microchip Test 2')
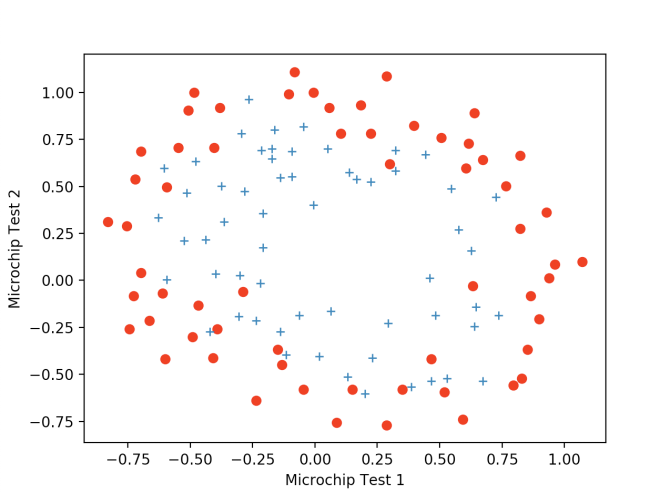
不难看到,此次的数据显然与之前几次的不大一样了,最明显的差别就是无法再用一条直线将这两类数据分开,直线已经无法满足分类了。那么显然,为了好的拟合,我们要做的就是增加θ,也就是要增加特征。
数据处理
将数据转成矩阵就不再多说了,在这里最关键的一步就是增加特征,得到一些更高次的特征来是我们的模型达到一个好的拟合效果,而增加多少次则是一个玄学…这里我们设置为6次项,至于原理需要以后再开一个专题讨论了。
def mapFeature(x1, x2):
power = 6
data = {}
for i in np.arange(power + 1):
for p in np.arange(i + 1):
data["f{}{}".format(i - p, p)] = np.power(x1, i - p) * np.power(x2, p)
return pd.DataFrame(data)
正则化
损失函数与梯度下降我们上期就讲过,而为什么要加入正则化呢我们之前也提到了,是为了防止过拟合。这些特征里面我们不知道哪些特征更为重要,于是选择不删除,而是用温柔的正则化保留特征,尽可能的减少影响,如果不记得正则化的公式那么就回顾一下:
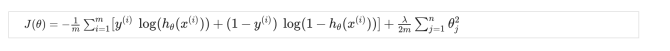

有了公式也就方便了许多,那么就将代码写出来吧:
# compute cost and grad
def costFunctionReg(theta_in, XX, yy):
lambda_in = 1
m = len(yy)
hypo = sigmoid(XX @ theta_in)
# print(sum(np.power(theta_in[1:len(theta_in)], 2)))
J = 1 / m * sum(-yy.T @ np.log(hypo) - (1 - yy).T @ (np.log(1 - hypo)))+(lambda_in / (2 * m) * sum(np.power(theta_in[1:len(theta_in)], 2)))
return J
结果展示
优化的方法与先前相同,我们所做的仅仅是加上了正则化项,来看看结果吧。
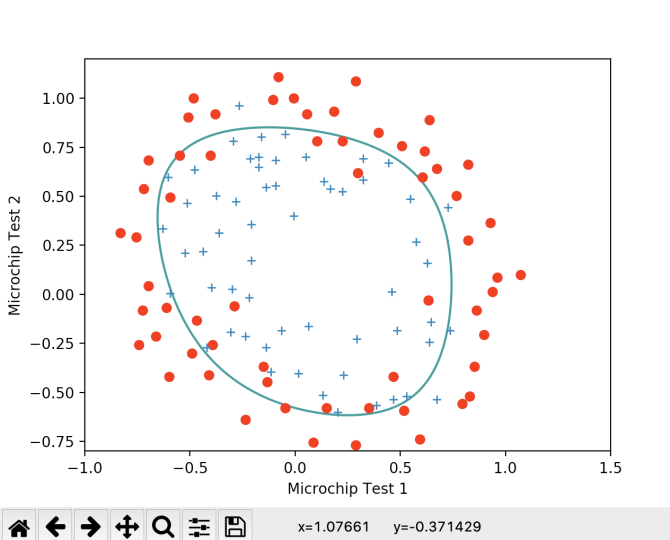
这样我们就得到了一个十分不错的分类,虽然有些点会有所偏差,但是它的泛化能力一定强于锱铢必较型的模型。
写在后面
那么正则化的逻辑回归也实现了,是不是感觉实现起来并没有那么难,那就试试吧。
