1. 前言
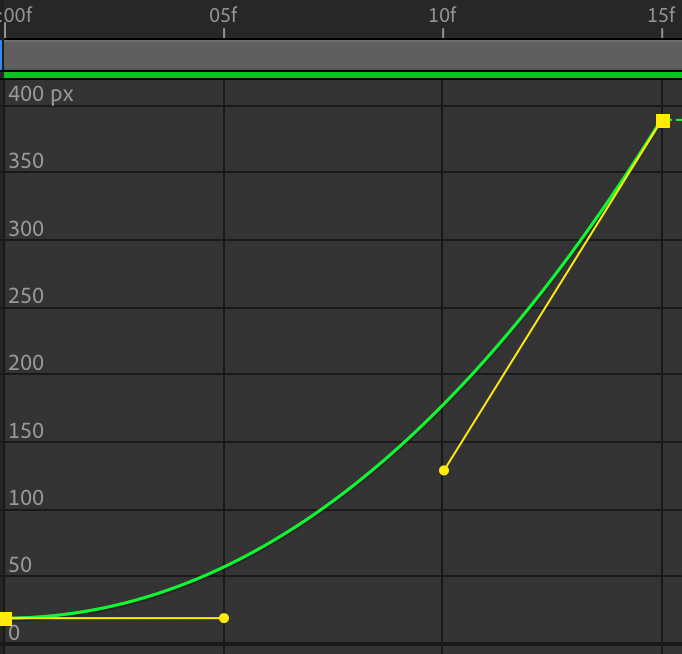 After Effects 中的运动曲线编辑器
After Effects 中的运动曲线编辑器
我们开始于这样一个图像,在各类 GUI 动画制作软件中,我们往往使用到了如上图所示的运动曲线图像来调整运动的效果,但是:
-
如何认知这类图像的真实意义,如何使用他们来达到我们想要的运动效果?
-
如果我们使用手动拖拽的方式,怎么放置锚点才能更接近我们需要的物理运动效果?
-
如果我们可以精确地用参数来设定锚点,又该怎样去得到合适的参数呢?
正如:设计的呈现可能是简单的,但是往往越简单的呈现代表的是越复杂的设计过程。这类动画曲线编辑器实在是过于常见,似乎也过于简单,但是这种简单呈现背后所蕴含的力量是如此强大,甚至能够让我们自己探索并一窥经典物理学大厦所建立的根基。
这篇文章准备用基本的运动学和动力学方式推导出运动函数图像的具体形式以解答问题 2,再结合贝塞尔算法推算如何拟合以解答问题 3,由此尝试给出一个我们看待模拟运动的视角。由于作者水平极其有限,因此我们仅以基础的位移时间相关的运动为例。涉及到的物理数学知识也仅限于高中水平,对于一些更深入,和更广泛的问题我们最多简单介绍。
如果看完本文的读者能够明白:一旦我们对各种动态效果有更深入的数学直觉和足够高度的物理认知,那么一切软件对动画的参数模拟都有其物理意义,一切对动画的算法模拟都有其数学形式,这些都是我们可以完全理解和构建的。那么,本文的目的就达到了。
2.什么是我们的问题
回到文首的图片,我们不难发现这其实是一个坐标系中的函数图像,其纵轴为某元素的位移,横轴即是时间。基本在所有动画制作的软件中,对运动构建的这类可调节的曲线都是如此形式,并且其横轴绝大部分都是时间,纵轴则可以有各种不同单位,如:速度。而这个图像本身,又是由贝塞尔锚点控制的曲线。
所以,我们如果想要得到一条符合真实运动的曲线,需要考虑的是两部分内容:
-
一个运动的图像应该是什么样的;
-
如何用贝塞尔来拟合一个图像。
这也是本文接下来的两块主要内容。
一旦有了方向,我们就可以按部就班开始了,首先我们从头开始开始捋一捋运动这回事:我们知道,宏观低速的非电磁运动可以由牛顿建立的经典力学很好地解释,在经典力学中,运动分解为运动学和动力学两部分。其中运动学是我们获取运动物体的信息,动力学则是我们如何去预测物体接下来的运动。如何去理解这两句话?

随便拿起手边一个物件(最好不要太大太重,或者脆弱、珍贵),然后上抛,如果这个物件对你而言不是一团垃圾,那么你应该会尝试去接住它。显然,这个物件在抛出时,它被你在某个高度施加了一个初始速度,最后在某段时间后落地,这些我们观察到的内容,这就是它的运动学信息(显然,我们并不关心其颜色、价值等)。而你打算伸手接住它,因为你知道它会先上升,然后下降,最后你把手伸到了你预测的位置尝试接住它(显然,此时我们也并不太关心你预测的正确与否),这就是它的动力学。
*如果你用一个杯子做了这个试验,然后它杯具了,那么你可以自豪的说:我获取到的运动学信息和我用来预测的动力学至少有一个错误了(我们暂时相信自己的大脑在正确的前提下总能够作出正确快速的运算,并且我们的肢体完全跟得上大脑的指令。这也是一种科学研究方法:不妨设,我们是个小天才)。
现在我们知道,我们应该获取一些关于运动物体的信息,但是有哪些信息?一般而言,信息取决于我们需要使用它们的场景,鉴于上一个例子可能让我们失去一些宝贵的个人物品,我们还是从最简单的模型开始入手:
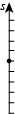
如上图所示,我们得到了一个一维的质点!并且在其所处的一维数轴上用刻度标示了它的位置!显然我们不会因为这个质点出了问题而失去什么!于是,我们得以放开手脚分析这个质点,来讨论如何构建我们的动力学了。首先,随着时间的流逝,它得动起来:
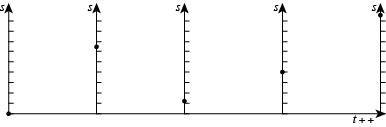
如果我们连续地体现出这个过程,那么我们就能得到一个图像,即位移随时间的关系图像: <math><semantics><mrow><mi>s</mi><mrow><mo fence="true">(</mo><mi>t</mi><mo fence="true">)</mo></mrow></mrow><annotation encoding="application/x-tex">s\left( t \right)</annotation></semantics></math>s(t) ,必须不能混淆的是,这个图像并不是质点的运动路径,质点本身是沿着数轴上下往复运动的:

呃,这不是一个美观优雅的图像,但是往好的方面看,我们发现了它和动画软件中的曲线编辑器的关系了:他们是同一种图像,因为他们具有同样的坐标系。也就是说如果我们搞清楚一个物体的运动如何体现在这种位移/速度/etc与时间的函数图像关系中,我们就知道这个曲线应该是什么样了,对应编辑出正确的曲线图,则我们就可以描述一个运动了。

如上图,这是一般曲线编辑器中都会直接预设的一种曲线模式,命名 Linear ,即线性的图像模式,不难发现,当我们将曲线设置成这样的时候,物体将以均匀不变的速度运动(当我们后面讨论完动力学表述之后,再回来看我们就会明白为什么这样就是均匀不变的速度)。
然而,自然的运动过程往往不是那么 Linear,我们需要更详细的剖析这个图像,以期能够编辑出正确的各种曲线。而在帮助我们理解图像这一点上,几乎所有的曲线编辑器往往都在偷懒:它们总是将带有图像笼统地用 easy-ease 形式命名,“渐入渐出”这类模糊主观的词语把运动推向了“感官和感觉”的深渊(很多设计领域已经在此深渊吃尽苦头)。
正如“节奏、动感”可以用“乐理、构成”对应和指导一样,运动,或者至少在虚拟世界中,运动是由数学和物理严格描述的。而“感觉“是一种高级的归类抽象,设计可以被外行用“感觉”描述,但设计师如果忽视思考和剖析,一味凭“感觉”行事,认识不到自己到底是在做什么,终究会迷惘。
3.图像(曲线编辑器)中有什么
我们知道,在这样一个单一维度的运动中,我们获取到的运动学信息是位置和时间,我们可以知道任何时间 <math><semantics><mrow><mi>t</mi></mrow><annotation encoding="application/x-tex">t</annotation></semantics></math>t 和该时刻对应的位移 <math><semantics><mrow><mi>s</mi><mrow><mo fence="true">(</mo><mi>t</mi><mo fence="true">)</mo></mrow></mrow><annotation encoding="application/x-tex">s\left( t \right)</annotation></semantics></math>s(t) ,但是这似乎不足以支撑起一个完整的动力学描述:我们无法预测下一刻的位置。换句话说,我们对 <math><semantics><mrow><mi>s</mi><mrow><mo fence="true">(</mo><mi>t</mi><mo fence="true">)</mo></mrow></mrow><annotation encoding="application/x-tex">s\left( t \right)</annotation></semantics></math>s(t) 的具体形式一无所知,无法计算也无法描绘它。
那么显然我们现在需要尝试推导出 <math><semantics><mrow><mi>s</mi><mrow><mo fence="true">(</mo><mi>t</mi><mo fence="true">)</mo></mrow></mrow><annotation encoding="application/x-tex">s\left( t \right)</annotation></semantics></math>s(t) 的形式,以获得关于这个图像的全部运动学信息,例如:我们在上节最后的例子那里知道,知道对于一个匀速运动的物体,这个 <math><semantics><mrow><mi>s</mi><mo>(</mo><mi>t</mi><mo>)</mo></mrow><annotation encoding="application/x-tex">s(t)</annotation></semantics></math>s(t) 就是一条直线的函数,这个函数的图像就是我们需要模拟匀速直线运动时的曲线。这里面蕴含了速度和初始位置,所以我们为什么仅需要这两个物理量就可以描述和预测一个匀速直线运动?
*小天才的直觉告诉我们,因为加速度等于零吖~但是,这个表述是否依然有点反直觉?我们需要由接下来的讨论建立一个真正的小天才般的直觉体系。
那么,除了时间和位移之外,一个位移/时间函数的图像中到底还含有什么其他的物理量?我们来试试速度:速度的定义是什么,我们知道 <math><semantics><mrow><mi>v</mi><mo>=</mo><mi>s</mi><mi mathvariant="normal">/</mi><mi>t</mi></mrow><annotation encoding="application/x-tex">v=s/t</annotation></semantics></math>v=s/t ,但是这是速度吗?我们先来试试如果我们这么做会得到什么:
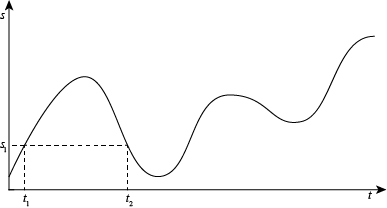
显然,<math><semantics><mrow><mfrac><mrow><msub><mi>s</mi><mrow><mn>1</mn></mrow></msub><mo>−</mo><msub><mi>s</mi><mrow><mn>1</mn></mrow></msub></mrow><mrow><msub><mi>t</mi><mrow><mn>2</mn></mrow></msub><mo>−</mo><msub><mi>t</mi><mrow><mn>1</mn></mrow></msub></mrow></mfrac><mo>=</mo><mn>0</mn></mrow><annotation encoding="application/x-tex">\frac{s_{1}-s_{1}}{t_{2}-t_{1}}=0</annotation></semantics></math>t2−t1s1−s1=0,那么是不是 <math><semantics><mrow><msub><mi>t</mi><mrow><mn>1</mn></mrow></msub></mrow><annotation encoding="application/x-tex">t_{1}</annotation></semantics></math>t1 到 <math><semantics><mrow><msub><mi>t</mi><mrow><mn>2</mn></mrow></msub></mrow><annotation encoding="application/x-tex">t_{2}</annotation></semantics></math>t2 这段时间的速度是 <math><semantics><mrow><mn>0</mn></mrow><annotation encoding="application/x-tex">0</annotation></semantics></math>0 呢?这当然不对,因为根据图像显示这段时间它仍然在运动。那么为什么呢,因为我们只选取了 <math><semantics><mrow><msub><mi>t</mi><mrow><mn>1</mn></mrow></msub></mrow><annotation encoding="application/x-tex">t_{1}</annotation></semantics></math>t1 和 <math><semantics><mrow><msub><mi>t</mi><mrow><mn>2</mn></mrow></msub></mrow><annotation encoding="application/x-tex">t_{2}</annotation></semantics></math>t2,没有选取它们间的任何其它时刻,因此也就无法代表任何时刻的速度,我们求出的只是一个时间段的平均速度。
平均速度无法完整地描述运动过程。而上文的加粗部分似乎在表达:我们只要选取所有时刻,就能够得到所有的速度。这似乎是一句废话,但是废话往往有很朴素的道理:如果我们知道任意时刻和它对应的位移,那其实就已经表达出 <math><semantics><mrow><mi>s</mi><mo>(</mo><mi>t</mi><mo>)</mo></mrow><annotation encoding="application/x-tex">s(t)</annotation></semantics></math>s(t) 了,因为函数 <math><semantics><mrow><mi>s</mi><mo>(</mo><mi>t</mi><mo>)</mo></mrow><annotation encoding="application/x-tex">s(t)</annotation></semantics></math>s(t) 就是 <math><semantics><mrow><mi>t</mi><mo>→</mo><mi>s</mi></mrow><annotation encoding="application/x-tex">t\rightarrow s</annotation></semantics></math>t→s 的映射。
这个废话的数学(不严谨)表述就是:位移就是速度对时间的积分,所以我们如果想要求速度,就需要对 <math><semantics><mrow><mi>s</mi><mo>(</mo><mi>t</mi><mo>)</mo></mrow><annotation encoding="application/x-tex">s(t)</annotation></semantics></math>s(t) 进行求导。同样的过程,速度是加速度对时间的积分,加速度就是对 <math><semantics><mrow><mi>v</mi><mo>(</mo><mi>t</mi><mo>)</mo></mrow><annotation encoding="application/x-tex">v(t)</annotation></semantics></math>v(t) 函数的求导。换句话我们可以这样说:速度是 <math><semantics><mrow><mi>s</mi><mo>(</mo><mi>t</mi><mo>)</mo></mrow><annotation encoding="application/x-tex">s(t)</annotation></semantics></math>s(t) 函数的一阶导数,加速度是 <math><semantics><mrow><mi>s</mi><mo>(</mo><mi>t</mi><mo>)</mo></mrow><annotation encoding="application/x-tex">s(t)</annotation></semantics></math>s(t) 函数的二阶导数。
*虽然我们前面设了:我们是小天才。但是可能有些时候我们过于天才导致自己跑得有点快,所以我们可以先不管积分、微分、导数这样的词汇,尝试朴素地体验一把凡人的思考过程(就是多说点废话)——当然,如果我们满足于自己的敏锐,就直接跳到下一节。
汽车的仪表盘无论何时都在告诉我们它现在的速度,它是如何做到的呢?我们知道 <math><semantics><mrow><mi>v</mi><mo>=</mo><mi>s</mi><mi mathvariant="normal">/</mi><mi>t</mi></mrow><annotation encoding="application/x-tex">v=s/t</annotation></semantics></math>v=s/t 这个式子只能够求出某一段位移的平均速度,那么我们如何用它找到任意时刻的速度?用极限的思维来看,只要我们选取的时间段足够短,这个时间段就越接近某一特定时刻,同时这段时间的运动状态变化也会更少。

由上图可以看出,如果 <math><semantics><mrow><msub><mi>t</mi><mrow><mn>2</mn></mrow></msub><mo>−</mo><msub><mi>t</mi><mrow><mn>1</mn></mrow></msub></mrow><annotation encoding="application/x-tex">t_{2}-t_{1}</annotation></semantics></math>t2−t1 越小,这一段的位移方式就越接近于匀速运动,平均速度就越接近于真实的瞬时速度。严谨起见,我们不能再用 <math><semantics><mrow><msub><mi>t</mi><mrow><mn>1</mn></mrow></msub></mrow><annotation encoding="application/x-tex">t_{1}</annotation></semantics></math>t1 和 <math><semantics><mrow><msub><mi>t</mi><mrow><mn>2</mn></mrow></msub></mrow><annotation encoding="application/x-tex">t_{2}</annotation></semantics></math>t2 这种表述方式,用极限的思维方式,我们定义 <math><semantics><mrow><msub><mi>t</mi><mrow><mn>2</mn></mrow></msub><mo>=</mo><msub><mi>t</mi><mrow><mn>1</mn></mrow></msub><mo>+</mo><mi mathvariant="normal">Δ</mi><mi>t</mi></mrow><annotation encoding="application/x-tex">t_{2}=t_{1}+\Delta t</annotation></semantics></math>t2=t1+Δt 和 <math><semantics><mrow><msub><mi>s</mi><mrow><mn>2</mn></mrow></msub><mo>=</mo><msub><mi>s</mi><mrow><mn>1</mn></mrow></msub><mo>+</mo><mi mathvariant="normal">Δ</mi><mi>s</mi></mrow><annotation encoding="application/x-tex">s_{2}=s_{1}+\Delta s</annotation></semantics></math>s2=s1+Δs ,这样我们就知道,对于给定的 <math><semantics><mrow><msub><mi>t</mi><mrow><mn>2</mn></mrow></msub></mrow><annotation encoding="application/x-tex">t_{2}</annotation></semantics></math>t2 时刻,其瞬时速度其实就是当 <math><semantics><mrow><mi mathvariant="normal">Δ</mi><mi>t</mi></mrow><annotation encoding="application/x-tex">\Delta t</annotation></semantics></math>Δt 趋近于 <math><semantics><mrow><mn>0</mn></mrow><annotation encoding="application/x-tex">0</annotation></semantics></math>0 时的 <math><semantics><mrow><mi mathvariant="normal">Δ</mi><mi>s</mi><mi mathvariant="normal">/</mi><mi mathvariant="normal">Δ</mi><mi>t</mi></mrow><annotation encoding="application/x-tex">\Delta s/\Delta t</annotation></semantics></math>Δs/Δt。
而这就是导数的极限定义: <math><semantics><mrow><msup><mi>s</mi><mrow><mi mathvariant="normal">′</mi></mrow></msup><mo>(</mo><mi>t</mi><mo>)</mo><mo>=</mo><mfrac><mrow><mi>d</mi><mi>s</mi></mrow><mrow><mi>d</mi><mi>t</mi></mrow></mfrac><mo>=</mo><msub><mi>lim</mi><mrow><mi mathvariant="normal">Δ</mi><mi>t</mi><mo>→</mo><mn>0</mn></mrow></msub><mfrac><mrow><mi mathvariant="normal">Δ</mi><mi>s</mi></mrow><mrow><mi mathvariant="normal">Δ</mi><mi>t</mi></mrow></mfrac></mrow><annotation encoding="application/x-tex">s'(t)=\frac{ds}{dt}=\lim_{\Delta t \rightarrow 0}\frac{\Delta s}{\Delta t}</annotation></semantics></math>s′(t)=dtds=limΔt→0ΔtΔs 。
现在我们知道,对于一个运动及其函数 <math><semantics><mrow><mi>s</mi><mo>(</mo><mi>t</mi><mo>)</mo></mrow><annotation encoding="application/x-tex">s(t)</annotation></semantics></math>s(t) 来说,其速度 <math><semantics><mrow><mi>v</mi><mo>=</mo><msup><mi>s</mi><mrow><mi mathvariant="normal">′</mi></mrow></msup><mo>(</mo><mi>t</mi><mo>)</mo></mrow><annotation encoding="application/x-tex">v=s'(t)</annotation></semantics></math>v=s′(t) ,其加速度 <math><semantics><mrow><mi>a</mi><mo>=</mo><msup><mi>s</mi><mrow><mi mathvariant="normal">′</mi><mi mathvariant="normal">′</mi></mrow></msup><mo>(</mo><mi>t</mi><mo>)</mo></mrow><annotation encoding="application/x-tex">a=s''(t)</annotation></semantics></math>a=s′′(t)。
那这对于我们找出 <math><semantics><mrow><mi>s</mi><mo>(</mo><mi>t</mi><mo>)</mo></mrow><annotation encoding="application/x-tex">s(t)</annotation></semantics></math>s(t) 是否有帮助呢?事实上不仅是帮助,而是这几乎就是任意形式的动力学描述需要的东西了。
4.匀加速运动的函数形式
我们现在开始寻找一类匀加速运动的数学表述,为什么是匀加速运动?首先,匀加速运动不论在生活还是动画中,都是最基础最广泛的存在——自由落体;其次,复杂的运动往往是简单运动的符合叠加,我们目前只需要最基本的例子;最后,匀加速运动含有刚好足够而不可减少的运动学信息。
我们不希望半路被打断,因此有必要先给出一个结论:对于 <math><semantics><mrow><mi>f</mi><mo>(</mo><mi>x</mi><mo>)</mo><mo>=</mo><mrow><msup><mi>x</mi><mi>n</mi></msup></mrow></mrow><annotation encoding="application/x-tex">f(x) = {x^n}</annotation></semantics></math>f(x)=xn ,我们有: <math><semantics><mrow><msup><mi>f</mi><mrow><mi mathvariant="normal">′</mi></mrow></msup><mo>(</mo><mi>x</mi><mo>)</mo><mo>=</mo><mi>n</mi><mrow><msup><mi>x</mi><mrow><mi>n</mi><mo>−</mo><mn>1</mn></mrow></msup></mrow></mrow><annotation encoding="application/x-tex">f'(x) = n{x^{n - 1}}</annotation></semantics></math>f′(x)=nxn−1 ,简单求导如下:
<math><semantics><mrow><mtable><mtr><mtd><mrow><msup><mi>f</mi><mrow><mi mathvariant="normal">′</mi></mrow></msup><mo>(</mo><mi>x</mi><mo>)</mo><mo>=</mo><mfrac><mrow><mrow><mrow><msup><mrow><mo>(</mo><mi>x</mi><mo>+</mo><mi mathvariant="normal">Δ</mi><mi>x</mi><mo>)</mo></mrow><mi>n</mi></msup></mrow><mo>−</mo><mrow><msup><mi>x</mi><mi>n</mi></msup></mrow></mrow></mrow><mrow><mrow><mo>(</mo><mi>x</mi><mo>+</mo><mi mathvariant="normal">Δ</mi><mi>x</mi><mo>)</mo><mo>−</mo><mi>x</mi></mrow></mrow></mfrac></mrow></mtd></mtr><mtr><mtd><mrow><mspace width="1em"></mspace><mspace width="1em"></mspace><mtext> </mtext><mo>=</mo><mfrac><mrow><mrow><msubsup><mi>C</mi><mi>n</mi><mn>0</mn></msubsup><mrow><msup><mi>x</mi><mi>n</mi></msup></mrow><mo>+</mo><msubsup><mi>C</mi><mi>n</mi><mn>1</mn></msubsup><mrow><msup><mi>x</mi><mrow><mi>n</mi><mo>−</mo><mn>1</mn></mrow></msup></mrow><mi mathvariant="normal">Δ</mi><mi>x</mi><mo>+</mo><mi mathvariant="normal">.</mi><mi mathvariant="normal">.</mi><mi mathvariant="normal">.</mi><mo>+</mo><msubsup><mi>C</mi><mi>n</mi><mi>n</mi></msubsup><mi mathvariant="normal">Δ</mi><mrow><msup><mi>x</mi><mi>n</mi></msup></mrow><mo>−</mo><mrow><msup><mi>x</mi><mi>n</mi></msup></mrow></mrow></mrow><mrow><mrow><mi mathvariant="normal">Δ</mi><mi>x</mi></mrow></mrow></mfrac></mrow></mtd></mtr><mtr><mtd><mrow><mspace width="1em"></mspace><mspace width="1em"></mspace><mtext> </mtext><mo>=</mo><msubsup><mi>C</mi><mi>n</mi><mn>1</mn></msubsup><mrow><msup><mi>x</mi><mrow><mi>n</mi><mo>−</mo><mn>1</mn></mrow></msup></mrow><mo>+</mo><msubsup><mi>C</mi><mi>n</mi><mn>2</mn></msubsup><mrow><msup><mi>x</mi><mrow><mi>n</mi><mo>−</mo><mn>2</mn></mrow></msup></mrow><mi mathvariant="normal">Δ</mi><mi>x</mi><mo>+</mo><mi mathvariant="normal">.</mi><mi mathvariant="normal">.</mi><mi mathvariant="normal">.</mi><mo>+</mo><msubsup><mi>C</mi><mi>n</mi><mi>n</mi></msubsup><mi mathvariant="normal">Δ</mi><mrow><msup><mi>x</mi><mrow><mi>n</mi><mo>−</mo><mn>1</mn></mrow></msup></mrow></mrow></mtd></mtr><mtr><mtd><mrow><mspace width="1em"></mspace><mspace width="1em"></mspace><mtext> </mtext><mo>=</mo><msubsup><mi>C</mi><mi>n</mi><mn>1</mn></msubsup><mrow><msup><mi>x</mi><mrow><mi>n</mi><mo>−</mo><mn>1</mn></mrow></msup></mrow><mo>+</mo><mi mathvariant="normal">Δ</mi><mi>x</mi><mo>(</mo><msubsup><mi>C</mi><mi>n</mi><mn>2</mn></msubsup><mrow><msup><mi>x</mi><mrow><mi>n</mi><mo>−</mo><mn>2</mn></mrow></msup></mrow><mo>+</mo><mi mathvariant="normal">.</mi><mi mathvariant="normal">.</mi><mi mathvariant="normal">.</mi><mo>+</mo><msubsup><mi>C</mi><mi>n</mi><mi>n</mi></msubsup><mi mathvariant="normal">Δ</mi><mrow><msup><mi>x</mi><mrow><mi>n</mi><mo>−</mo><mn>2</mn></mrow></msup></mrow><mo>)</mo></mrow></mtd></mtr></mtable></mrow><annotation encoding="application/x-tex">\begin{array}{l} f'(x) = \frac{{{{(x + \Delta x)}^n} - {x^n}}}{{(x + \Delta x) - x}}\\ \quad \quad \ = \frac{{C_n^0{x^n} + C_n^1{x^{n - 1}}\Delta x + ... + C_n^n\Delta {x^n} - {x^n}}}{{\Delta x}}\\ \quad \quad \ = C_n^1{x^{n - 1}} + C_n^2{x^{n - 2}}\Delta x + ... + C_n^n\Delta {x^{n - 1}}\\ \quad \quad \ = C_n^1{x^{n - 1}} + \Delta x(C_n^2{x^{n - 2}} + ... + C_n^n\Delta {x^{n - 2}}) \end{array}</annotation></semantics></math>f′(x)=(x+Δx)−x(x+Δx)n−xn =ΔxCn0xn+Cn1xn−1Δx+...+CnnΔxn−xn =Cn1xn−1+Cn2xn−2Δx+...+CnnΔxn−1 =Cn1xn−1+Δx(Cn2xn−2+...+CnnΔxn−2)
显然,当 <math><semantics><mrow><mi mathvariant="normal">Δ</mi><mi>x</mi><mo>→</mo><mn>0</mn></mrow><annotation encoding="application/x-tex">\Delta x \to 0</annotation></semantics></math>Δx→0 时,
<math><semantics><mrow><msup><mi>f</mi><mrow><mi mathvariant="normal">′</mi></mrow></msup><mo>(</mo><mi>x</mi><mo>)</mo><mo>=</mo><msubsup><mi>C</mi><mi>n</mi><mn>1</mn></msubsup><mrow><msup><mi>x</mi><mrow><mi>n</mi><mo>−</mo><mn>1</mn></mrow></msup></mrow><mo>=</mo><mi>n</mi><mrow><msup><mi>x</mi><mrow><mi>n</mi><mo>−</mo><mn>1</mn></mrow></msup></mrow></mrow><annotation encoding="application/x-tex">f'(x) = C_n^1{x^{n - 1}} = n{x^{n - 1}}</annotation></semantics></math>f′(x)=Cn1xn−1=nxn−1
这对于我们有什么帮助呢?我们先来看如果我们想要描绘一个匀加速运动的图像,我们需要获得哪些信息:对于一个匀加速运动,我们显然知道它有一个加速度:<math><semantics><mrow><msub><mi>a</mi><mrow><mn>0</mn></mrow></msub></mrow><annotation encoding="application/x-tex">a_{0}</annotation></semantics></math>a0,那么我们还需要什么其它的信息来构建 <math><semantics><mrow><mi>s</mi><mo>(</mo><mi>t</mi><mo>)</mo></mrow><annotation encoding="application/x-tex">s(t)</annotation></semantics></math>s(t) 呢?我们可以用一个例子来看:一个自由下坠的小球。那么似乎我们有一个给定的高度 <math><semantics><mrow><mi>h</mi></mrow><annotation encoding="application/x-tex">h</annotation></semantics></math>h ,一个初始的速度 <math><semantics><mrow><mn>0</mn></mrow><annotation encoding="application/x-tex">0</annotation></semantics></math>0 ……但是这是一个针对特例的猜测过程,很不严谨。
我们转化一下问题:我们需要哪些物理量来确定一个一般化的匀加速运动的动力学表达?那么再回头审视在一个匀加速运动中我们确定一定有的是什么?是 <math><semantics><mrow><mi>a</mi><mo>=</mo><msub><mi>a</mi><mrow><mn>0</mn></mrow></msub></mrow><annotation encoding="application/x-tex">a=a_{0}</annotation></semantics></math>a=a0,还有呢?嗯……
嗯?
没了!?

但是,不慌,我们之前花了不少篇幅推了那些个结论,正是因为我们早就料到有这么一天(先射箭,再画靶),我们用小天才一般的沉着冷静,结合前文结论,不紧不慢书写如下:
<math><semantics><mrow><mtable><mtr><mtd><mrow><mi>a</mi><mo>=</mo><msup><mi>s</mi><mrow><mi mathvariant="normal">′</mi><mi mathvariant="normal">′</mi></mrow></msup><mo>(</mo><mi>t</mi><mo>)</mo><mo>=</mo><msub><mi>a</mi><mrow><mn>0</mn></mrow></msub></mrow></mtd></mtr><mtr><mtd><mrow><mi>v</mi><mo>=</mo><msup><mi>s</mi><mrow><mi mathvariant="normal">′</mi></mrow></msup><mo>(</mo><mi>t</mi><mo>)</mo></mrow></mtd></mtr><mtr><mtd><mrow><mi>s</mi><mo>=</mo><mi>s</mi><mo>(</mo><mi>t</mi><mo>)</mo></mrow></mtd></mtr></mtable></mrow><annotation encoding="application/x-tex">\begin{array}{l} a=s''(t)=a_{0} \\v=s'(t) \\ s=s(t) \end{array}</annotation></semantics></math>a=s′′(t)=a0v=s′(t)s=s(t)
显然,这个问题就是,已知 <math><semantics><mrow><msup><mi>s</mi><mrow><mi mathvariant="normal">′</mi><mi mathvariant="normal">′</mi></mrow></msup><mo>(</mo><mi>t</mi><mo>)</mo></mrow><annotation encoding="application/x-tex">s''(t)</annotation></semantics></math>s′′(t) 求 <math><semantics><mrow><msup><mi>s</mi><mrow><mi mathvariant="normal">′</mi></mrow></msup><mo>(</mo><mi>t</mi><mo>)</mo></mrow><annotation encoding="application/x-tex">s'(t)</annotation></semantics></math>s′(t) 、<math><semantics><mrow><mi>s</mi><mo>(</mo><mi>t</mi><mo>)</mo></mrow><annotation encoding="application/x-tex">s(t)</annotation></semantics></math>s(t),那么我们在前一页防打断的结论可以直接用了:
我们把
<math><semantics><mrow><msup><mi>s</mi><mrow><mi mathvariant="normal">′</mi><mi mathvariant="normal">′</mi></mrow></msup><mo>(</mo><mi>t</mi><mo>)</mo><mo>=</mo><msub><mi>a</mi><mrow><mn>0</mn></mrow></msub></mrow><annotation encoding="application/x-tex">s''(t)=a_{0}</annotation></semantics></math>s′′(t)=a0
按照前文导数的形式,写成和其自变量有关的形式
<math><semantics><mrow><msup><mi>s</mi><mrow><mi mathvariant="normal">′</mi><mi mathvariant="normal">′</mi></mrow></msup><mo>(</mo><mi>t</mi><mo>)</mo><mo>=</mo><msub><mi>a</mi><mrow><mn>0</mn></mrow></msub><mo>=</mo><msub><mi>a</mi><mrow><mn>0</mn></mrow></msub><mo>⋅</mo><mi>n</mi><msup><mi>t</mi><mrow><mi>n</mi><mo>−</mo><mn>1</mn></mrow></msup></mrow><annotation encoding="application/x-tex">s''(t)=a_{0}=a_{0}\cdot nt^{n-1}</annotation></semantics></math>s′′(t)=a0=a0⋅ntn−1
不难发现,我们立即有
<math><semantics><mrow><mi>n</mi><mo>=</mo><mn>1</mn></mrow><annotation encoding="application/x-tex">n=1</annotation></semantics></math>n=1
则
<math><semantics><mrow><msup><mi>s</mi><mrow><mi mathvariant="normal">′</mi></mrow></msup><mo>(</mo><mi>t</mi><mo>)</mo><mo>=</mo><msub><mi>a</mi><mrow><mn>0</mn></mrow></msub><mi>t</mi></mrow><annotation encoding="application/x-tex">s'(t)=a_{0}t</annotation></semantics></math>s′(t)=a0t ①
但是,我们注意到,如果对一个常量求导如
<math><semantics><mrow><mi>f</mi><mo>(</mo><mi>x</mi><mo>)</mo><mo>=</mo><mn>3</mn><mo>=</mo><mn>3</mn><msup><mi>x</mi><mrow><mn>0</mn></mrow></msup></mrow><annotation encoding="application/x-tex">f(x)=3=3x^{0}</annotation></semantics></math>f(x)=3=3x0
则
<math><semantics><mrow><msup><mi>f</mi><mrow><mi mathvariant="normal">′</mi></mrow></msup><mo>(</mo><mi>x</mi><mo>)</mo><mo>=</mo><mn>0</mn></mrow><annotation encoding="application/x-tex">f'(x)=0</annotation></semantics></math>f′(x)=0
因此我们可以在①式中加入任意常量,而不影响 <math><semantics><mrow><msup><mi>s</mi><mrow><mi mathvariant="normal">′</mi><mi mathvariant="normal">′</mi></mrow></msup><mo>(</mo><mi>t</mi><mo>)</mo></mrow><annotation encoding="application/x-tex">s''(t)</annotation></semantics></math>s′′(t)
<math><semantics><mrow><msup><mi>s</mi><mrow><mi mathvariant="normal">′</mi></mrow></msup><mo>(</mo><mi>t</mi><mo>)</mo><mo>=</mo><msub><mi>a</mi><mrow><mn>0</mn></mrow></msub><mi>t</mi><mo>+</mo><mi>b</mi></mrow><annotation encoding="application/x-tex">s'(t)=a_{0}t+b</annotation></semantics></math>s′(t)=a0t+b
那么再继续如上过程
<math><semantics><mrow><msup><mi>s</mi><mrow><mi mathvariant="normal">′</mi></mrow></msup><mo>(</mo><mi>t</mi><mo>)</mo><mo>=</mo><msub><mi>a</mi><mrow><mn>0</mn></mrow></msub><mi>t</mi><mo>+</mo><mi>b</mi><mo>=</mo><msub><mi>a</mi><mrow><mn>0</mn></mrow></msub><mo>⋅</mo><mi>n</mi><msup><mi>t</mi><mrow><mi>n</mi><mo>−</mo><mn>1</mn></mrow></msup><mo>+</mo><mi>b</mi><mo>⋅</mo><mi>m</mi><msup><mi>t</mi><mrow><mi>m</mi><mo>−</mo><mn>1</mn></mrow></msup><mo>+</mo><mn>0</mn></mrow><annotation encoding="application/x-tex">s'(t)=a_{0}t+b=a_{0}\cdot nt^{n-1}+b\cdot mt^{m-1}+0</annotation></semantics></math>s′(t)=a0t+b=a0⋅ntn−1+b⋅mtm−1+0
显然,我们立刻就有:
<math><semantics><mrow><mi>n</mi><mo>=</mo><mn>2</mn><mo separator="true">,</mo><mtext> </mtext><mtext> </mtext><mi>m</mi><mo>=</mo><mn>1</mn></mrow><annotation encoding="application/x-tex">n=2,\ \ m=1</annotation></semantics></math>n=2, m=1
但是这会导致 <math><semantics><mrow><msup><mi>s</mi><mrow><mi mathvariant="normal">′</mi></mrow></msup><mo>(</mo><mi>t</mi><mo>)</mo></mrow><annotation encoding="application/x-tex">s'(t)</annotation></semantics></math>s′(t) 中出现 <math><semantics><mrow><mn>2</mn><msub><mi>a</mi><mrow><mn>0</mn></mrow></msub></mrow><annotation encoding="application/x-tex">2a_{0}</annotation></semantics></math>2a0,所以我们需要添加一个 <math><semantics><mrow><mn>1</mn><mi mathvariant="normal">/</mi><mn>2</mn></mrow><annotation encoding="application/x-tex">1/2</annotation></semantics></math>1/2 的系数:
<math><semantics><mrow><mi>s</mi><mo>(</mo><mi>t</mi><mo>)</mo><mo>=</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac><msub><mi>a</mi><mrow><mn>0</mn></mrow></msub><msup><mi>t</mi><mrow><mn>2</mn></mrow></msup><mo>+</mo><mi>b</mi><mi>t</mi><mo>+</mo><mi>c</mi></mrow><annotation encoding="application/x-tex">s(t)=\frac{1}{2}a_{0}t^{2}+bt+c</annotation></semantics></math>s(t)=21a0t2+bt+c
*上述过程实际上是一个粗糙的计算积分的过程,我们没有采用积分的描述方法来运算,因为积分的运算很容易就会变得不太……人道,但是最主要的原因是我们小天才般的认为,在目前的简单运动中并无需要引入过多复杂的数学工具(๑•̀ㅂ•́) ✧
现在,我们得到了如下描述
<math><semantics><mrow><mi>a</mi><mo>=</mo><msup><mi>s</mi><mrow><mi mathvariant="normal">′</mi><mi mathvariant="normal">′</mi></mrow></msup><mo>(</mo><mi>t</mi><mo>)</mo><mo>=</mo><msub><mi>a</mi><mrow><mn>0</mn></mrow></msub></mrow><annotation encoding="application/x-tex">a=s''(t)=a_{0}</annotation></semantics></math>a=s′′(t)=a0
<math><semantics><mrow><mi>v</mi><mo>=</mo><msup><mi>s</mi><mrow><mi mathvariant="normal">′</mi></mrow></msup><mo>(</mo><mi>t</mi><mo>)</mo><mo>=</mo><msub><mi>a</mi><mrow><mn>0</mn></mrow></msub><mi>t</mi><mo>+</mo><mi>b</mi></mrow><annotation encoding="application/x-tex">v=s'(t)=a_{0}t+b</annotation></semantics></math>v=s′(t)=a0t+b
<math><semantics><mrow><mi>s</mi><mo>=</mo><mi>s</mi><mo>(</mo><mi>t</mi><mo>)</mo><mo>=</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac><msub><mi>a</mi><mrow><mn>0</mn></mrow></msub><msup><mi>t</mi><mrow><mn>2</mn></mrow></msup><mo>+</mo><mi>b</mi><mi>t</mi><mo>+</mo><mi>c</mi></mrow><annotation encoding="application/x-tex">s=s(t)=\frac{1}{2}a_{0}t^{2}+bt+c</annotation></semantics></math>s=s(t)=21a0t2+bt+c
但是,我们不太满意,因为式子里面出现了 b 和 c 两个我们为了补全积分而引入的常量系数,这两个量是什么玩意儿?让我们消除掉所有其他量,来看看这两个莫名出现的量到底等于什么:
显然,如果我们令 <math><semantics><mrow><mi>t</mi><mo>=</mo><mn>0</mn></mrow><annotation encoding="application/x-tex">t=0</annotation></semantics></math>t=0,则立刻有
<math><semantics><mrow><mi>v</mi><mo>=</mo><mi>b</mi></mrow><annotation encoding="application/x-tex">v=b</annotation></semantics></math>v=b
<math><semantics><mrow><mi>s</mi><mo>=</mo><mi>c</mi></mrow><annotation encoding="application/x-tex">s=c</annotation></semantics></math>s=c
所以 <math><semantics><mrow><mi>b</mi></mrow><annotation encoding="application/x-tex">b</annotation></semantics></math>b 实际就是初始时刻物体所具有的初速度 <math><semantics><mrow><msub><mi>v</mi><mrow><mn>0</mn></mrow></msub></mrow><annotation encoding="application/x-tex">v_{0}</annotation></semantics></math>v0 ;而 <math><semantics><mrow><mi>c</mi></mrow><annotation encoding="application/x-tex">c</annotation></semantics></math>c 就是初始时刻物体的初始位置 <math><semantics><mrow><msub><mi>s</mi><mrow><mn>0</mn></mrow></msub></mrow><annotation encoding="application/x-tex">s_{0}</annotation></semantics></math>s0 。那么我们可以将一个匀加速运动一般化如下:
<math><semantics><mrow><mi>s</mi><mo>(</mo><mi>t</mi><mo>)</mo><mo>=</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac><msub><mi>a</mi><mrow><mn>0</mn></mrow></msub><msup><mi>t</mi><mrow><mn>2</mn></mrow></msup><mo>+</mo><msub><mi>v</mi><mrow><mn>0</mn></mrow></msub><mi>t</mi><mo>+</mo><msub><mi>s</mi><mrow><mn>0</mn></mrow></msub></mrow><annotation encoding="application/x-tex">s(t)=\frac{1}{2}a_{0}t^{2}+v_{0}t+s_{0}</annotation></semantics></math>s(t)=21a0t2+v0t+s0
由这个一般通式,可以看出,描述一个匀加速运动,我们需要三个量:一个不变的加速度、物体初速度、物体初始位置,只要有这三个量,我们就可以预测这个物体在任意时刻的位置了。
不用怀疑我们的天才,这就是任意匀加速运动的通式了,如果我们对其有矢量性(方向)和适用性(宏观低速)等本质的一些怀疑,首先要恭喜自己已经具有相当强的数学和物理直觉,不过鉴于我们不希望跑题,这一部分如果有机会,就放到最后再简单说一说。
*即使在数学上来看,这个式子也非常容易理解,一个匀加速物体在任意时刻的位移由三部分贡献:物体的初始位移、物体初速度对时间的积分、物体加速度对时间的重积分。
5.小球弹跳对应的曲线表示
现在我们通过令人发困的长篇大论知道了一个通用的匀加速运动的动力学描述了,那么,这种描述如何指导我们编辑出与这类运动相符的曲线呢?
 错误示例
错误示例我们现在可以用具体的例子试一下,以期看到本质:在一个自由坠落弹跳的小球运动中,我们可以以初始位置为坐标原点,并且让小球从静止开始坠落,这样也就没有了初速度和初始位移。那么这样一个小球坠落的最终动力学表述是: <math><semantics><mrow><mi>s</mi><mo>=</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac><mi>a</mi><msup><mi>t</mi><mrow><mn>2</mn></mrow></msup></mrow><annotation encoding="application/x-tex">s=\frac{1}{2}at^{2}</annotation></semantics></math>s=21at2
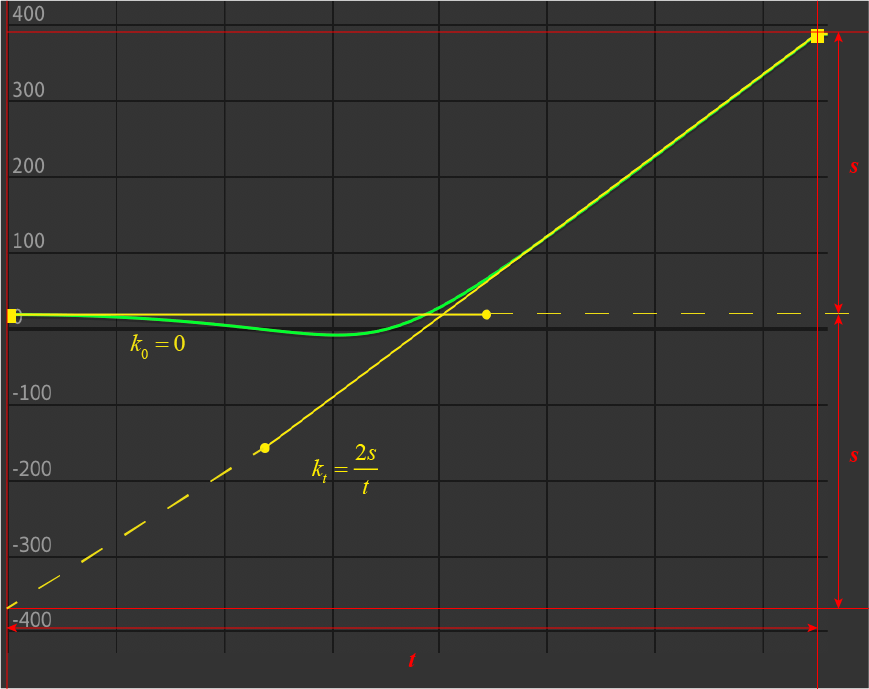
很不巧,我们在设定动画的时候,可以通过开始和结束位置设定 <math><semantics><mrow><mi>s</mi></mrow><annotation encoding="application/x-tex">s</annotation></semantics></math>s ,而且显然一个动画的时间 <math><semantics><mrow><mi>t</mi></mrow><annotation encoding="application/x-tex">t</annotation></semantics></math>t 也是我们自由决定的,但是我们没有一个加速度 <math><semantics><mrow><mi>a</mi></mrow><annotation encoding="application/x-tex">a</annotation></semantics></math>a 。
那该怎么办?自然的坠落,在直观上似乎是由加速度和位置决定了下落所用的时间:<math><semantics><mrow><mi>t</mi><mo>=</mo><msqrt><mrow><mfrac><mrow><mn>2</mn><mi>s</mi></mrow><mrow><mi>a</mi></mrow></mfrac></mrow></msqrt></mrow><annotation encoding="application/x-tex">t=\sqrt{\frac{2s}{a}}</annotation></semantics></math>t=√a2s,因为我们不能改变的是加速度。
但是在软件中我们没有加速度,不过我们可以以一种和自然不同的方式来变换这个式子: <math><semantics><mrow><mi>a</mi><mo>=</mo><mfrac><mrow><mn>2</mn><mi>s</mi></mrow><mrow><msup><mi>t</mi><mrow><mn>2</mn></mrow></msup></mrow></mfrac></mrow><annotation encoding="application/x-tex">a=\frac{2s}{t^{2}}</annotation></semantics></math>a=t22s ,这个式子的物理意义似乎是:当我们设定了一个自由落体运动的位移,也设定了坠落持续的时间,则加速度就是确定的了。对应的也就是说,当我们设定好位移和时间后,一个小球坠落的动力学函数就有着唯一的图像了。
 一旦这个曲线的起末位置被设定,符合自由落体的曲线就有且只有一条了
一旦这个曲线的起末位置被设定,符合自由落体的曲线就有且只有一条了那么我们如何去拟合这条图像?我们观察到两条黄色锚杆本质是在曲线终末处的切线。
*当然这又是天才般的直觉!锚杆是该点的切线是由贝塞尔算法决定的,可以通过对贝塞尔基函数求一阶导证明,不过由于这部分对本文毫无意义,我们在这里直接拿来主义。
鉴于我们之前已经回忆了一些极限和导师的东西,我们敏锐地记起了课本定义:一个函数任意一点的导数是函数在该点切线的斜率。前面我们已经发现了,匀加速运动在任意时刻的一阶导数就是该时刻的速度,所以两根锚杆的斜率不过就是终末两点的速度而已!我们立刻奋笔疾书如下:
<math><semantics><mrow><msub><mi>v</mi><mrow><mn>0</mn></mrow></msub><mo>=</mo><mn>0</mn></mrow><annotation encoding="application/x-tex">v_{0}=0</annotation></semantics></math>v0=0
<math><semantics><mrow><msub><mi>v</mi><mrow><mi>t</mi></mrow></msub><mo>=</mo><mi>a</mi><mi>t</mi><mo>=</mo><mfrac><mrow><mn>2</mn><mi>s</mi></mrow><mrow><mi>t</mi></mrow></mfrac></mrow><annotation encoding="application/x-tex">v_{t}=at=\frac{2s}{t}</annotation></semantics></math>vt=at=t2s
天才如我们又立刻在曲线编辑器中遵循该式作出如下曲线设定:
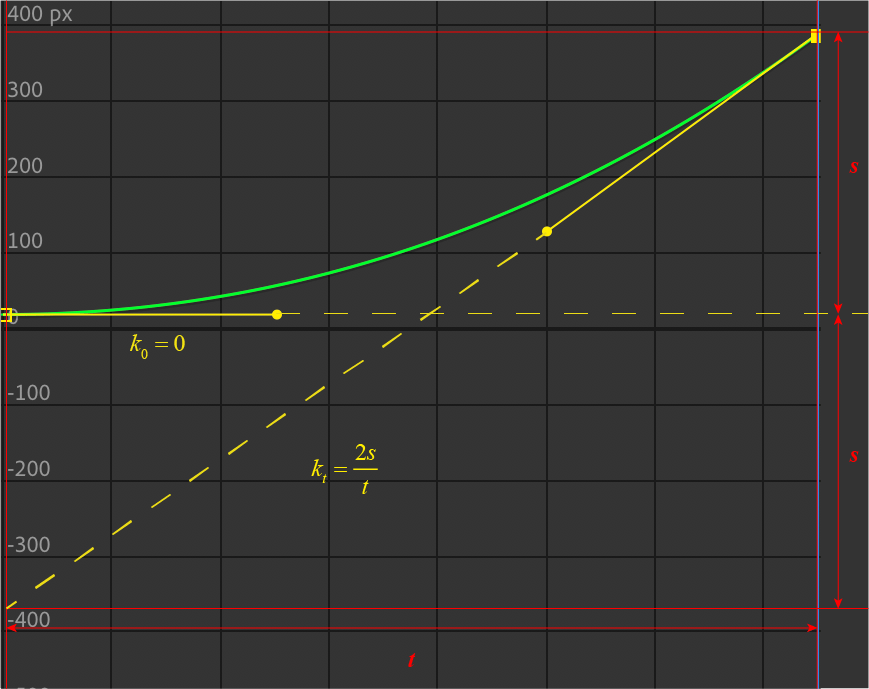 锚杆的斜率为对应点的速度
锚杆的斜率为对应点的速度
运行看看!
非常自然,任谁都可以看出这就是坠落!太好了,似乎我们终于在不知所云的纷乱中找到了答案!
但是这是完整的吗?这个问题由锚杆末端的黄色小球提出,它们不太满意上述内容把它们当空气,于是它们做了如下变换:
斜率还是速度,但是曲线却不再是我们希望的那条曲线了,这就非常令人沮丧和恼火,这俩玩意儿是什么时候冒出来的?它们似乎完全没有物理意义,那我们该怎么看待它们呢?
6.参数化曲线——贝塞尔曲线算法
虽然我们更想从以上的运动学分析说开,来让自己“探索并一窥经典物理学大厦所建立的根基”,但是鉴于我们之前信誓旦旦地要让自己严格地描述,所以还是有必要专门说一说贝塞尔曲线,有关“物理”的私货就往本篇的文末挤一挤吧。如果对贝塞尔曲线有足够的认识,或者并不是很想关心这类算法,仅想知道如何来控制贝塞尔曲线使其满足一个从静止开始的匀加速运动,那么可以跳到本节最后几段,那里有我们的结论。
有必要事先声明的是:
1.贝塞尔曲线方程实质上就是一类多项式参数方程,其不仅应用于动画曲线,事实上它是计算机图形学中一类相当重要的参数曲线,并且大部分设计软件中都或多或少有所应用(在一些更专业的设计软件中或许并非构造曲线的主要工具),在代码实现中,也有非常广泛的应用。因此这部分讨论其实已经相当超纲,如果只是为了知道一类运动曲线的具体形态特征,那么我们在前文中讨论的内容基本已经大致足够。
2.对于贝塞尔曲线的理解作者本身还比较初级,因此接下来的讨论并不会向上文那样能够以小天才一般的直觉(并不)比较直观地从基础开始分析推导,而是照本宣科,简单用自己的理解推算到三次贝塞尔,其中可能会存在比上文中更不严谨的乃至于可以称之为错误的表述。
3.如果你看到了这里,并且决定继续深入讨论这一部分内容,那么有一个作者认为其实从一开始就应该提出的问题需要我们思考:是什么支撑着我们跟着这篇这半懂不懂,不精不通的文章走下去的?真的只是为了得到最后那个简单的结论来操作一条贝塞尔曲线吗(这个结论甚至比上文物理的方式更加简单和易于操作)?
那么回到正题,我们发现图像中这两个锚点是没有任何物理意义的,因此只能借助纯粹的数学来尝试解读锚点,这就是贝塞尔曲线。思路和之前一样,我们需要找到锚点的数学表述,以及弄清楚它们对我们的曲线是如何施加影响的。
我们先从一条线的基本属性看起,对于二维上任一段曲线来说,我们首先会有其起点和终点:
<math><semantics><mrow><mrow><msub><mi>P</mi><mn>0</mn></msub></mrow><mo>[</mo><mtable><mtr><mtd><mrow><mrow><mrow><msub><mi>x</mi><mn>0</mn></msub></mrow></mrow></mrow></mtd><mtd><mrow><mrow><mrow><msub><mi>y</mi><mn>0</mn></msub></mrow></mrow></mrow></mtd></mtr></mtable><mo>]</mo></mrow><annotation encoding="application/x-tex">{P_0}[\begin{array}{l} {{x_0}}&{{y_0}} \end{array}]</annotation></semantics></math>P0[x0y0]
<math><semantics><mrow><mrow><msub><mi>P</mi><mn>1</mn></msub></mrow><mo>[</mo><mtable><mtr><mtd><mrow><mrow><mrow><msub><mi>x</mi><mn>1</mn></msub></mrow></mrow></mrow></mtd><mtd><mrow><mrow><mrow><msub><mi>y</mi><mn>1</mn></msub></mrow></mrow></mrow></mtd></mtr></mtable><mo>]</mo></mrow><annotation encoding="application/x-tex">{P_1}[\begin{array}{l} {{x_1}}&{{y_1}} \end{array}]</annotation></semantics></math>P1[x1y1]
我们先来看最简单的线性贝塞尔,也就是当我们决定 <math><semantics><mrow><msub><mi>P</mi><mrow><mn>0</mn></mrow></msub><msub><mi>P</mi><mrow><mn>1</mn></mrow></msub></mrow><annotation encoding="application/x-tex">P_{0}P_{1}</annotation></semantics></math>P0P1 是一条直线段时,我们是如何用数学从起点到终点来描述这个线段的。需要注意的是,我们现在寻求的是一类能够描述该线段上任意点的算法,并非仅仅是由终末点求直线,只有这样我们才能扩展更高阶贝塞尔算法。这和之前我们寻求速度一样,我们需要知道一条曲线上每一个点都是怎么来的,才能构建其算法。为便于理解,我们看如下的示意图:
我们发现可以直接代入前文运动学的讨论来看待这条线段上的某点 <math><semantics><mrow><mi>B</mi></mrow><annotation encoding="application/x-tex">B</annotation></semantics></math>B,在这里,我们不需要考虑速度,可以直接理解如下:点 <math><semantics><mrow><mi>B</mi></mrow><annotation encoding="application/x-tex">B</annotation></semantics></math>B 以匀速从起始时间 <math><semantics><mrow><mn>0</mn></mrow><annotation encoding="application/x-tex">0</annotation></semantics></math>0 运动到终末时间 <math><semantics><mrow><mn>1</mn></mrow><annotation encoding="application/x-tex">1</annotation></semantics></math>1 所积得的路径即为 <math><semantics><mrow><msub><mi>P</mi><mrow><mn>0</mn></mrow></msub><msub><mi>P</mi><mrow><mn>1</mn></mrow></msub></mrow><annotation encoding="application/x-tex">P_{0}P_{1}</annotation></semantics></math>P0P1 。
则我们可以列式如下:
<math><semantics><mrow><msub><mi>P</mi><mrow><mn>0</mn></mrow></msub><mi>B</mi><mo>:</mo><msub><mi>P</mi><mrow><mn>0</mn></mrow></msub><msub><mi>P</mi><mrow><mn>1</mn></mrow></msub><mo>=</mo><mi>t</mi><mo separator="true">,</mo><mtext> </mtext><mtext> </mtext><mtext> </mtext><mi>t</mi><mo>∈</mo><mo>[</mo><mn>0</mn><mo separator="true">,</mo><mn>1</mn><mo>]</mo></mrow><annotation encoding="application/x-tex">P_{0}B:P_{0}P_{1}=t,\ \ \ t\in[0,1]</annotation></semantics></math>P0B:P0P1=t, t∈[0,1]
<math><semantics><mrow><msub><mi>P</mi><mrow><mn>0</mn></mrow></msub><mi>B</mi><mo>=</mo><mi>B</mi><mo>−</mo><msub><mi>P</mi><mrow><mn>0</mn></mrow></msub></mrow><annotation encoding="application/x-tex">P_{0}B=B-P_{0}</annotation></semantics></math>P0B=B−P0
<math><semantics><mrow><msub><mi>P</mi><mrow><mn>0</mn></mrow></msub><msub><mi>P</mi><mrow><mn>1</mn></mrow></msub><mo>=</mo><msub><mi>P</mi><mrow><mn>1</mn></mrow></msub><mo>−</mo><msub><mi>P</mi><mrow><mn>0</mn></mrow></msub></mrow><annotation encoding="application/x-tex">P_{0}P_{1}=P_{1}-P_{0}</annotation></semantics></math>P0P1=P1−P0
联立上述式子,可得点 <math><semantics><mrow><mi>B</mi></mrow><annotation encoding="application/x-tex">B</annotation></semantics></math>B 关于 <math><semantics><mrow><mi>t</mi></mrow><annotation encoding="application/x-tex">t</annotation></semantics></math>t 的表达式,即为 <math><semantics><mrow><mi>B</mi><mo>(</mo><mi>t</mi><mo>)</mo></mrow><annotation encoding="application/x-tex">B(t)</annotation></semantics></math>B(t) :
<math><semantics><mrow><mtable><mtr><mtd><mrow><mi>B</mi><mo>(</mo><mi>t</mi><mo>)</mo><mo>=</mo><mo>(</mo><mrow><msub><mi>P</mi><mn>1</mn></msub></mrow><mo>−</mo><mrow><msub><mi>P</mi><mn>0</mn></msub></mrow><mo>)</mo><mi>t</mi><mo>+</mo><mrow><msub><mi>P</mi><mn>0</mn></msub></mrow><mo separator="true">,</mo><mtext> </mtext><mtext> </mtext><mtext> </mtext><mtext> </mtext><mtext> </mtext><mi>t</mi><mo>∈</mo><mo>[</mo><mn>0</mn><mo separator="true">,</mo><mn>1</mn><mo>]</mo></mrow></mtd></mtr><mtr><mtd><mrow><mi>B</mi><mo>(</mo><mi>t</mi><mo>)</mo><mo>=</mo><mo>(</mo><mn>1</mn><mo>−</mo><mi>t</mi><mo>)</mo><mrow><msub><mi>P</mi><mn>0</mn></msub></mrow><mo>+</mo><mi>t</mi><mrow><msub><mi>P</mi><mn>1</mn></msub></mrow><mo separator="true">,</mo><mtext> </mtext><mtext> </mtext><mtext> </mtext><mtext> </mtext><mtext> </mtext><mtext> </mtext><mi>t</mi><mo>∈</mo><mo>[</mo><mn>0</mn><mo separator="true">,</mo><mn>1</mn><mo>]</mo></mrow></mtd></mtr></mtable></mrow><annotation encoding="application/x-tex">\begin{array}{l} B(t) = ({P_1} - {P_0})t + {P_0},\ \ \ \ \ t \in [0,1]\\ B(t) = (1 - t){P_0} + t{P_1},\ \ \ \ \ \ t \in [0,1] \end{array}</annotation></semantics></math>B(t)=(P1−P0)t+P0, t∈[0,1]B(t)=(1−t)P0+tP1, t∈[0,1]
这样,我们就有了线性贝塞尔算法的表达了,在 <math><semantics><mrow><mo>[</mo><mn>0</mn><mo separator="true">,</mo><mn>1</mn><mo>]</mo></mrow><annotation encoding="application/x-tex">[0,1]</annotation></semantics></math>[0,1] 上的任一 <math><semantics><mrow><mi>t</mi></mrow><annotation encoding="application/x-tex">t</annotation></semantics></math>t ,都对应存在一个点 <math><semantics><mrow><mi>B</mi></mrow><annotation encoding="application/x-tex">B</annotation></semantics></math>B ,所有点 <math><semantics><mrow><mi>B</mi></mrow><annotation encoding="application/x-tex">B</annotation></semantics></math>B 所积得的路径,即为该算法由终末点画出的曲线 <math><semantics><mrow><msub><mi>P</mi><mrow><mn>0</mn></mrow></msub><msub><mi>P</mi><mrow><mn>1</mn></mrow></msub></mrow><annotation encoding="application/x-tex">P_{0}P_{1}</annotation></semantics></math>P0P1 。因为这是线性贝塞尔算法,所以体现为一个线段。
注意到我们列出了两个式子,这样做的原因是第一种表述方式是能够直观展示其矩阵形式的:
<math><semantics><mrow><mi>B</mi><mo>(</mo><mi>t</mi><mo>)</mo><mo>=</mo><mrow><mo fence="true">(</mo><mrow><mtable><mtr><mtd><mrow><mi>t</mi></mrow></mtd><mtd><mrow><mn>1</mn></mrow></mtd></mtr></mtable></mrow><mo fence="true">)</mo></mrow><mrow><mo fence="true">(</mo><mrow><mtable><mtr><mtd><mrow><mrow><mo>−</mo><mn>1</mn></mrow></mrow></mtd><mtd><mrow><mn>1</mn></mrow></mtd></mtr><mtr><mtd><mrow><mn>1</mn></mrow></mtd><mtd><mrow><mn>0</mn></mrow></mtd></mtr></mtable></mrow><mo fence="true">)</mo></mrow><mrow><mo fence="true">(</mo><mrow><mtable><mtr><mtd><mrow><mrow><mrow><msub><mi>P</mi><mn>0</mn></msub></mrow></mrow></mrow></mtd></mtr><mtr><mtd><mrow><mrow><mrow><msub><mi>P</mi><mn>1</mn></msub></mrow></mrow></mrow></mtd></mtr></mtable></mrow><mo fence="true">)</mo></mrow></mrow><annotation encoding="application/x-tex">B(t) = \left( {\begin{array}{l} t&1 \end{array}} \right)\left( {\begin{array}{l} { - 1}&1\\ 1&0 \end{array}} \right)\left( {\begin{array}{l} {{P_0}}\\ {{P_1}} \end{array}} \right)</annotation></semantics></math>B(t)=(t1)(−1110)(P0P1)
而第二种则更偏向代数上的理解: <math><semantics><mrow><mi>t</mi></mrow><annotation encoding="application/x-tex">t</annotation></semantics></math>t 在由 <math><semantics><mrow><mn>0</mn></mrow><annotation encoding="application/x-tex">0</annotation></semantics></math>0 到 <math><semantics><mrow><mn>1</mn></mrow><annotation encoding="application/x-tex">1</annotation></semantics></math>1 的变化过程中,是如何对各点施加不同影响从而得到点 <math><semantics><mrow><mi>B</mi></mrow><annotation encoding="application/x-tex">B</annotation></semantics></math>B 的。
*两种理解方式各有优劣,第一种方式能够让我们从更高维度的视角去认识曲线、曲面等全部涉及到向量和空间的内容,同样也可以成为我们看待运动学和动力学的更高维视角,因为线性代数的本质就是向量和线性空间的线性变换。但是如果对此并无涉猎打算,那么就可以以第二种方式,从字面意义上简单理解即可。
线性贝塞尔只能够描绘直线段,显然我们并不满足于此,所以我们要开始往更高阶行进:二次贝塞尔算法。
现在我们希望曲线 [{P_0}{P_1}] 上的点 B 不仅仅积出一条线段,而是真正意义的曲线(曲率不为零),那么依照上文,一定有一个关于 t 的比例关系成立,在哪里找到 t ?
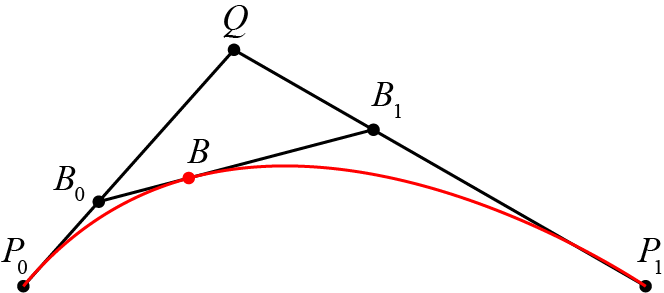
我们在终末点之外另加一点 <math><semantics><mrow><mi>Q</mi></mrow><annotation encoding="application/x-tex">Q</annotation></semantics></math>Q ,不难看出,线段 <math><semantics><mrow><msub><mi>P</mi><mrow><mn>0</mn></mrow></msub><mi>Q</mi></mrow><annotation encoding="application/x-tex">P_{0}Q</annotation></semantics></math>P0Q 和线段 <math><semantics><mrow><mi>Q</mi><msub><mi>P</mi><mrow><mn>1</mn></mrow></msub></mrow><annotation encoding="application/x-tex">QP_{1}</annotation></semantics></math>QP1 分别是由线性贝塞尔算出的线段,其中有:<math><semantics><mrow><msub><mi>P</mi><mrow><mn>0</mn></mrow></msub><msub><mi>B</mi><mrow><mn>0</mn></mrow></msub><mo>:</mo><msub><mi>P</mi><mrow><mn>0</mn></mrow></msub><mi>Q</mi><mo>=</mo><mi>Q</mi><msub><mi>B</mi><mrow><mn>1</mn></mrow></msub><mo>:</mo><mi>Q</mi><msub><mi>P</mi><mrow><mn>1</mn></mrow></msub><mo>=</mo><mi>t</mi></mrow><annotation encoding="application/x-tex">P_{0}B_{0}:P_{0}Q=QB_{1}:QP_{1}=t</annotation></semantics></math>P0B0:P0Q=QB1:QP1=t,在这样的基础上,我们在 <math><semantics><mrow><msub><mi>B</mi><mrow><mn>0</mn></mrow></msub><msub><mi>B</mi><mrow><mn>1</mn></mrow></msub></mrow><annotation encoding="application/x-tex">B_{0}B_{1}</annotation></semantics></math>B0B1 上寻求一个点 <math><semantics><mrow><mi>B</mi></mrow><annotation encoding="application/x-tex">B</annotation></semantics></math>B 使得<math><semantics><mrow><msub><mi>B</mi><mrow><mn>0</mn></mrow></msub><mi>B</mi><mo>:</mo><msub><mi>B</mi><mrow><mn>0</mn></mrow></msub><msub><mi>B</mi><mrow><mn>1</mn></mrow></msub><mo>=</mo><mi>t</mi></mrow><annotation encoding="application/x-tex">B_{0}B:B_{0}B_{1}=t</annotation></semantics></math>B0B:B0B1=t,则随着 <math><semantics><mrow><mi>t</mi></mrow><annotation encoding="application/x-tex">t</annotation></semantics></math>t 从 <math><semantics><mrow><mn>0</mn></mrow><annotation encoding="application/x-tex">0</annotation></semantics></math>0 增加到 <math><semantics><mrow><mn>1</mn></mrow><annotation encoding="application/x-tex">1</annotation></semantics></math>1 ,这样的点 <math><semantics><mrow><mi>B</mi></mrow><annotation encoding="application/x-tex">B</annotation></semantics></math>B 积成的曲线就是二次贝塞尔曲线(不难看出为什么是“二次”,因为我们做了两次线性贝塞尔运算)。
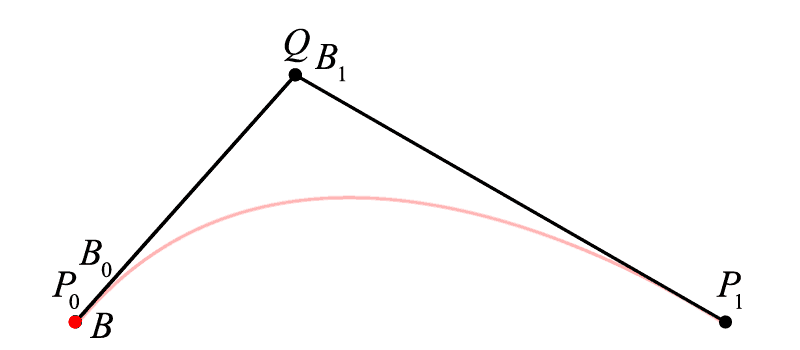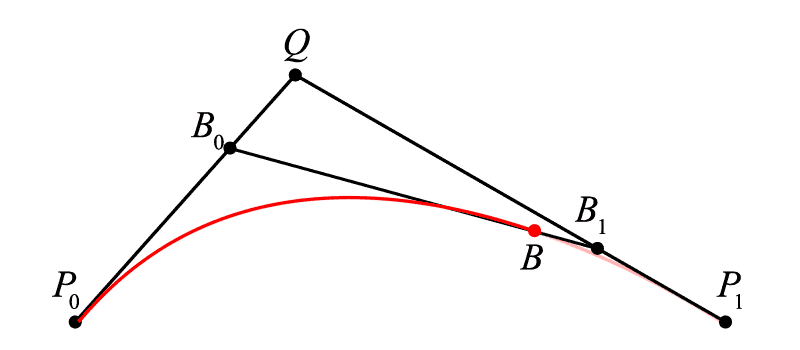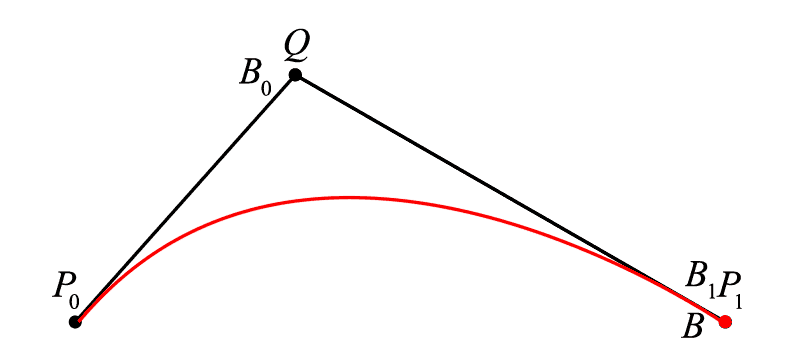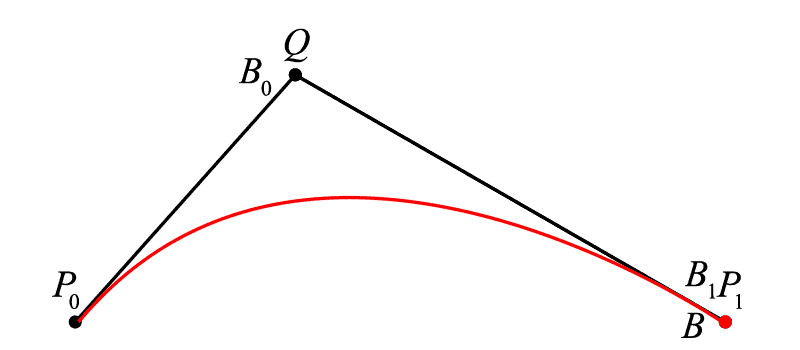 二次贝塞尔描绘过程
二次贝塞尔描绘过程
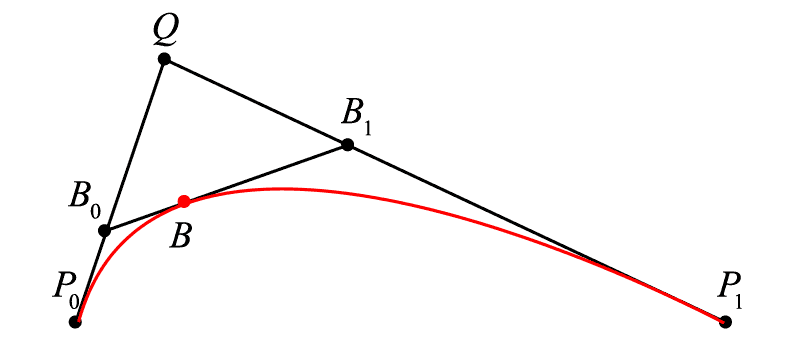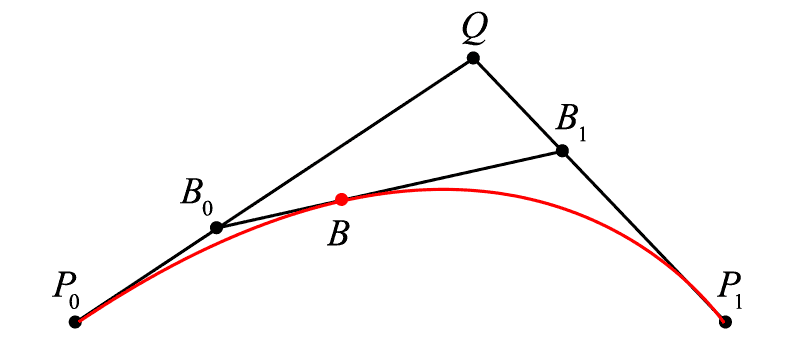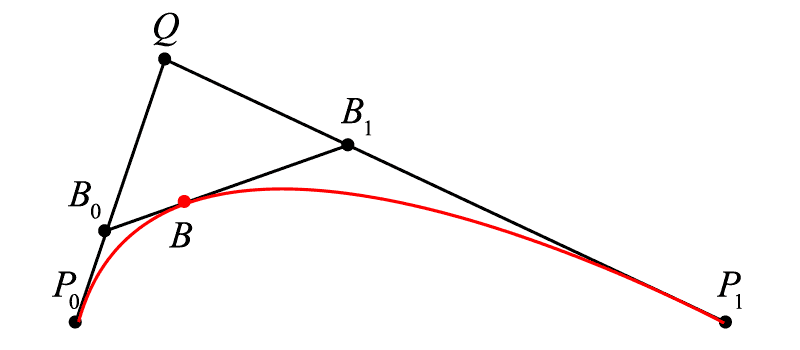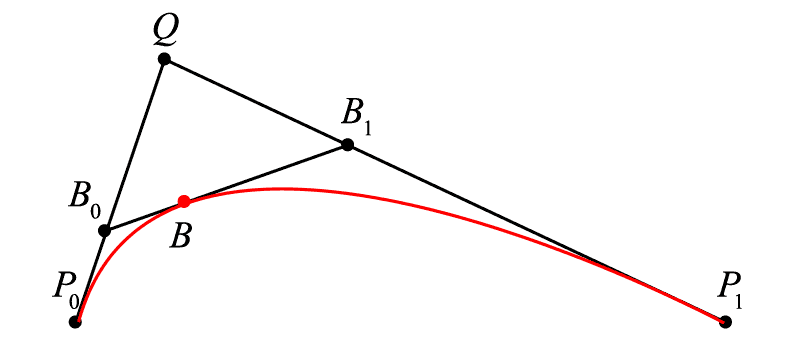 通过移动点 Q 来改变曲线的形态
通过移动点 Q 来改变曲线的形态
参照前文,我们直接就有 <math><semantics><mrow><msub><mi>B</mi><mrow><mn>0</mn></mrow></msub><mo separator="true">,</mo><msub><mi>B</mi><mrow><mn>1</mn></mrow></msub><mo separator="true">,</mo><mi>B</mi></mrow><annotation encoding="application/x-tex">B_{0},B_{1},B</annotation></semantics></math>B0,B1,B 的表达式:
<math><semantics><mrow><msub><mi>B</mi><mrow><mn>0</mn></mrow></msub><mo>=</mo><mo>(</mo><mi>Q</mi><mo>−</mo><msub><mi>P</mi><mrow><mn>0</mn></mrow></msub><mo>)</mo><mi>t</mi><mo>+</mo><msub><mi>P</mi><mrow><mn>0</mn></mrow></msub></mrow><annotation encoding="application/x-tex">B_{0}=(Q-P_{0})t+P_{0}</annotation></semantics></math>B0=(Q−P0)t+P0
<math><semantics><mrow><msub><mi>B</mi><mrow><mn>1</mn></mrow></msub><mo>=</mo><mo>(</mo><msub><mi>P</mi><mrow><mn>1</mn></mrow></msub><mo>−</mo><mi>Q</mi><mo>)</mo><mi>t</mi><mo>+</mo><mi>Q</mi></mrow><annotation encoding="application/x-tex">B_{1}=(P_{1}-Q)t+Q</annotation></semantics></math>B1=(P1−Q)t+Q
<math><semantics><mrow><mi>B</mi><mo>=</mo><mo>(</mo><msub><mi>B</mi><mrow><mn>1</mn></mrow></msub><mo>−</mo><msub><mi>B</mi><mrow><mn>0</mn></mrow></msub><mo>)</mo><mi>t</mi><mo>+</mo><msub><mi>B</mi><mrow><mn>0</mn></mrow></msub></mrow><annotation encoding="application/x-tex">B=(B_{1}-B_{0})t+B_{0}</annotation></semantics></math>B=(B1−B0)t+B0
联立上述方程轻松可得如下二次贝塞尔表达式:
<math><semantics><mrow><mi>B</mi><mo>(</mo><mi>t</mi><mo>)</mo><mo>=</mo><mrow><mo fence="true">(</mo><mrow><mtable><mtr><mtd><mrow><mrow><mrow><msup><mi>t</mi><mn>2</mn></msup></mrow></mrow></mrow></mtd><mtd><mrow><mi>t</mi></mrow></mtd><mtd><mrow><mn>1</mn></mrow></mtd></mtr></mtable></mrow><mo fence="true">)</mo></mrow><mrow><mo fence="true">(</mo><mrow><mtable><mtr><mtd><mrow><mn>1</mn></mrow></mtd><mtd><mrow><mrow><mo>−</mo><mn>2</mn></mrow></mrow></mtd><mtd><mrow><mn>1</mn></mrow></mtd></mtr><mtr><mtd><mrow><mrow><mo>−</mo><mn>2</mn></mrow></mrow></mtd><mtd><mrow><mn>2</mn></mrow></mtd><mtd><mrow><mn>0</mn></mrow></mtd></mtr><mtr><mtd><mrow><mn>1</mn></mrow></mtd><mtd><mrow><mn>0</mn></mrow></mtd><mtd><mrow><mn>0</mn></mrow></mtd></mtr></mtable></mrow><mo fence="true">)</mo></mrow><mrow><mo fence="true">(</mo><mrow><mtable><mtr><mtd><mrow><mrow><mrow><msub><mi>P</mi><mn>0</mn></msub></mrow></mrow></mrow></mtd></mtr><mtr><mtd><mrow><mi>Q</mi></mrow></mtd></mtr><mtr><mtd><mrow><mrow><mrow><msub><mi>P</mi><mn>1</mn></msub></mrow></mrow></mrow></mtd></mtr></mtable></mrow><mo fence="true">)</mo></mrow><mo separator="true">,</mo><mi>t</mi><mo>∈</mo><mo>[</mo><mn>0</mn><mo separator="true">,</mo><mn>1</mn><mo>]</mo></mrow><annotation encoding="application/x-tex">B(t) = \left( {\begin{array}{l} {{t^2}}&t&1 \end{array}} \right)\left( {\begin{array}{l} 1&{ - 2}&1\\ { - 2}&2&0\\ 1&0&0 \end{array}} \right)\left( {\begin{array}{l} {{P_0}}\\ Q\\ {{P_1}} \end{array}} \right), t \in [0,1]</annotation></semantics></math>B(t)=(t2t1)⎝⎛1−21−220100⎠⎞⎝⎛P0QP1⎠⎞,t∈[0,1]
<math><semantics><mrow><mi>B</mi><mo>(</mo><mi>t</mi><mo>)</mo><mo>=</mo><mrow><mo>(</mo><mn>1</mn><mo>−</mo><mi>t</mi><msup><mo>)</mo><mn>2</mn></msup></mrow><mrow><msub><mi>P</mi><mn>0</mn></msub></mrow><mo>+</mo><mn>2</mn><mi>t</mi><mo>(</mo><mn>1</mn><mo>−</mo><mi>t</mi><mo>)</mo><mi>Q</mi><mo>+</mo><mrow><msup><mi>t</mi><mn>2</mn></msup></mrow><mrow><msub><mi>P</mi><mn>1</mn></msub></mrow><mo separator="true">,</mo><mtext> </mtext><mtext> </mtext><mtext> </mtext><mtext> </mtext><mi>t</mi><mo>∈</mo><mo>[</mo><mn>0</mn><mo separator="true">,</mo><mn>1</mn><mo>]</mo></mrow><annotation encoding="application/x-tex">B(t) = {(1 - t)^2}{P_0} + 2t(1 - t)Q + {t^2}{P_1},\ \ \ \ t \in [0,1]</annotation></semantics></math>B(t)=(1−t)2P0+2t(1−t)Q+t2P1, t∈[0,1]
那么三次贝塞尔简直呼之欲出,仅需要再增加一次线性贝塞尔套娃:
<math><semantics><mrow><mi>B</mi><mo>(</mo><mi>t</mi><mo>)</mo><mo>=</mo><mrow><mo fence="true">(</mo><mrow><mrow><msup><mi>t</mi><mn>3</mn></msup></mrow><mtable><mtr><mtd><mrow><mrow><mrow><msup><mi>t</mi><mn>2</mn></msup></mrow></mrow></mrow></mtd><mtd><mrow><mi>t</mi></mrow></mtd><mtd><mrow><mn>1</mn></mrow></mtd></mtr></mtable></mrow><mo fence="true">)</mo></mrow><mrow><mo fence="true">(</mo><mrow><mtable><mtr><mtd><mrow><mrow><mo>−</mo><mn>1</mn></mrow></mrow></mtd><mtd><mrow><mn>3</mn></mrow></mtd><mtd><mrow><mrow><mo>−</mo><mn>3</mn></mrow></mrow></mtd><mtd><mrow><mn>1</mn></mrow></mtd></mtr><mtr><mtd><mrow><mn>3</mn></mrow></mtd><mtd><mrow><mrow><mo>−</mo><mn>6</mn></mrow></mrow></mtd><mtd><mrow><mn>3</mn></mrow></mtd><mtd><mrow><mn>0</mn></mrow></mtd></mtr><mtr><mtd><mrow><mrow><mo>−</mo><mn>3</mn></mrow></mrow></mtd><mtd><mrow><mn>3</mn></mrow></mtd><mtd><mrow><mn>0</mn></mrow></mtd><mtd><mrow><mn>0</mn></mrow></mtd></mtr><mtr><mtd><mrow><mn>1</mn></mrow></mtd><mtd><mrow><mn>0</mn></mrow></mtd><mtd><mrow><mn>0</mn></mrow></mtd><mtd><mrow><mn>0</mn></mrow></mtd></mtr></mtable></mrow><mo fence="true">)</mo></mrow><mrow><mo fence="true">(</mo><mrow><mtable><mtr><mtd><mrow><mrow><mrow><msub><mi>P</mi><mn>0</mn></msub></mrow></mrow></mrow></mtd></mtr><mtr><mtd><mrow><mrow><mrow><msub><mi>Q</mi><mn>0</mn></msub></mrow></mrow></mrow></mtd></mtr><mtr><mtd><mrow><mrow><mrow><msub><mi>Q</mi><mn>1</mn></msub></mrow></mrow></mrow></mtd></mtr><mtr><mtd><mrow><mrow><mrow><msub><mi>P</mi><mn>1</mn></msub></mrow></mrow></mrow></mtd></mtr></mtable></mrow><mo fence="true">)</mo></mrow><mo separator="true">,</mo><mi>t</mi><mo>∈</mo><mo>[</mo><mn>0</mn><mo separator="true">,</mo><mn>1</mn><mo>]</mo></mrow><annotation encoding="application/x-tex">B(t) = \left( {{t^3}\begin{array}{l} {{t^2}}&t&1 \end{array}} \right)\left( {\begin{array}{l} { - 1}&3&{ - 3}&1\\ 3&{ - 6}&3&0\\ { - 3}&3&0&0\\ 1&0&0&0 \end{array}} \right)\left( {\begin{array}{l} {{P_0}}\\ {{Q_0}}\\ {{Q_1}}\\ {{P_1}} \end{array}} \right),t \in [0,1]</annotation></semantics></math>B(t)=(t3t2t1)⎝⎜⎜⎛−13−313−630−33001000⎠⎟⎟⎞⎝⎜⎜⎛P0Q0Q1P1⎠⎟⎟⎞,t∈[0,1]
<math><semantics><mrow><mi>B</mi><mo>(</mo><mi>t</mi><mo>)</mo><mo>=</mo><mrow><mo>(</mo><mn>1</mn><mo>−</mo><mi>t</mi><msup><mo>)</mo><mn>3</mn></msup></mrow><mrow><msub><mi>P</mi><mn>0</mn></msub></mrow><mo>+</mo><mn>3</mn><mi>t</mi><mrow><mo>(</mo><mn>1</mn><mo>−</mo><mi>t</mi><msup><mo>)</mo><mn>2</mn></msup></mrow><mrow><msub><mi>Q</mi><mn>0</mn></msub></mrow><mo>+</mo><mn>3</mn><mrow><msup><mi>t</mi><mn>2</mn></msup></mrow><mo>(</mo><mn>1</mn><mo>−</mo><mi>t</mi><mo>)</mo><mrow><msub><mi>Q</mi><mn>1</mn></msub></mrow><mo>+</mo><mrow><msup><mi>t</mi><mn>3</mn></msup></mrow><mrow><msub><mi>P</mi><mn>1</mn></msub></mrow><mo separator="true">,</mo><mtext> </mtext><mtext> </mtext><mtext> </mtext><mtext> </mtext><mi>t</mi><mo>∈</mo><mo>[</mo><mn>0</mn><mo separator="true">,</mo><mn>1</mn><mo>]</mo></mrow><annotation encoding="application/x-tex">B(t) = {(1 - t)^3}{P_0} + 3t{(1 - t)^2}{Q_0} + 3{t^2}(1 - t){Q_1} + {t^3}{P_1},\ \ \ \ t \in [0,1]</annotation></semantics></math>B(t)=(1−t)3P0+3t(1−t)2Q0+3t2(1−t)Q1+t3P1, t∈[0,1]
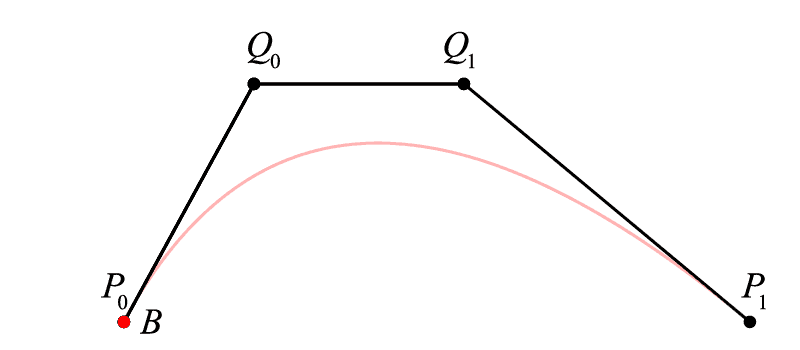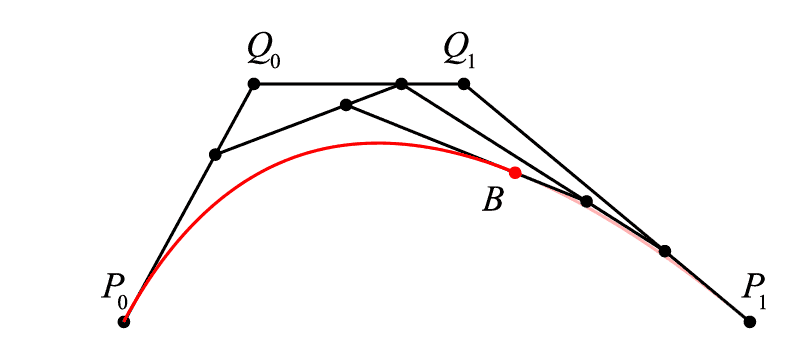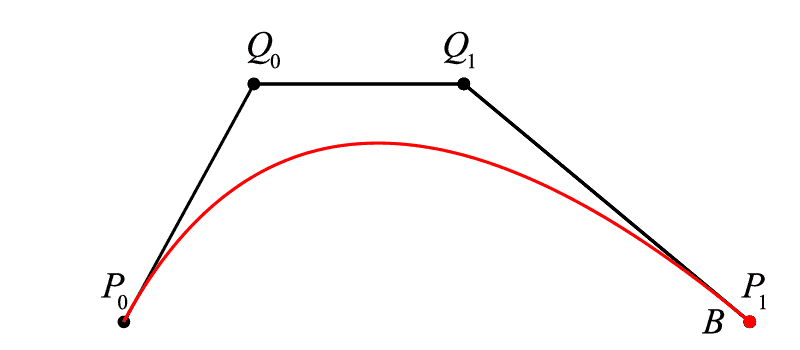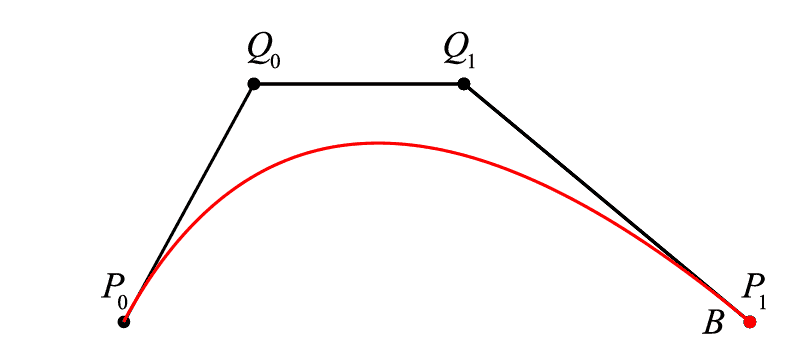
三次贝塞尔描绘过程
这部分的推算我们就略去不表,和由线性贝塞尔扩展到二次贝塞尔没有什么区别,重要的是,我们立刻观察到 <math><semantics><mrow><msub><mi>P</mi><mrow><mn>0</mn></mrow></msub><msub><mi>Q</mi><mrow><mn>0</mn></mrow></msub></mrow><annotation encoding="application/x-tex">P_{0}Q_{0}</annotation></semantics></math>P0Q0 和 <math><semantics><mrow><msub><mi>P</mi><mrow><mn>1</mn></mrow></msub><msub><mi>Q</mi><mrow><mn>1</mn></mrow></msub></mrow><annotation encoding="application/x-tex">P_{1}Q_{1}</annotation></semantics></math>P1Q1 的特殊,它们似乎和我们的曲线有着很亲近的关系:
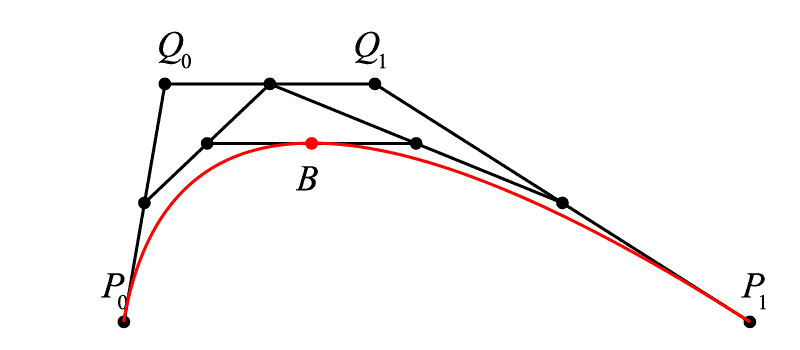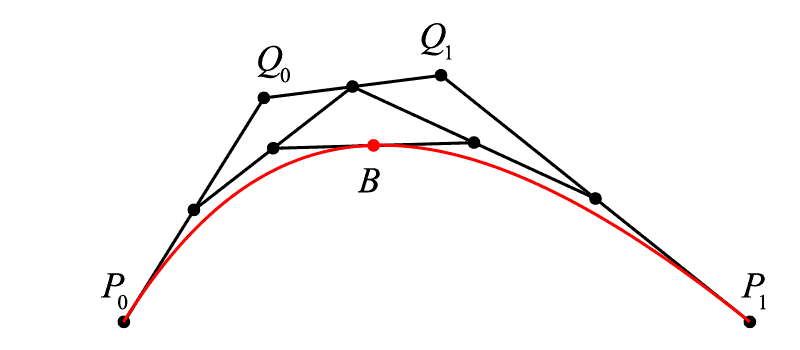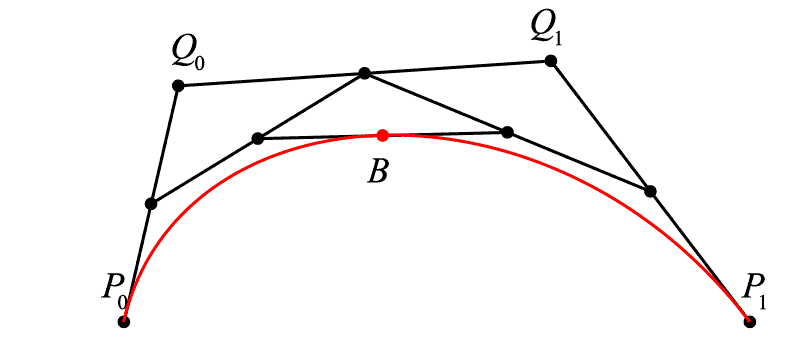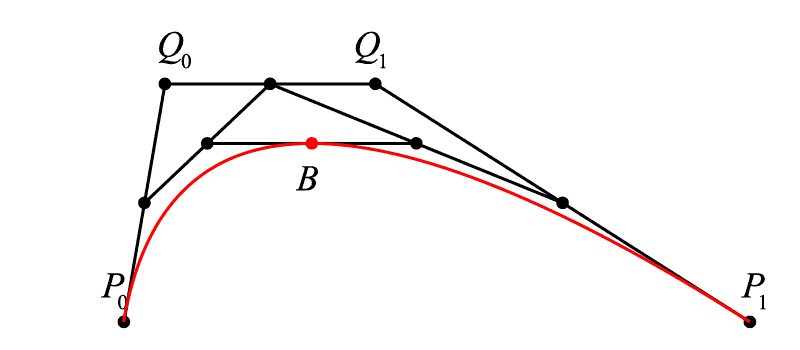 通过移动点 Q0 和 Q1 来改变曲线的形态
通过移动点 Q0 和 Q1 来改变曲线的形态
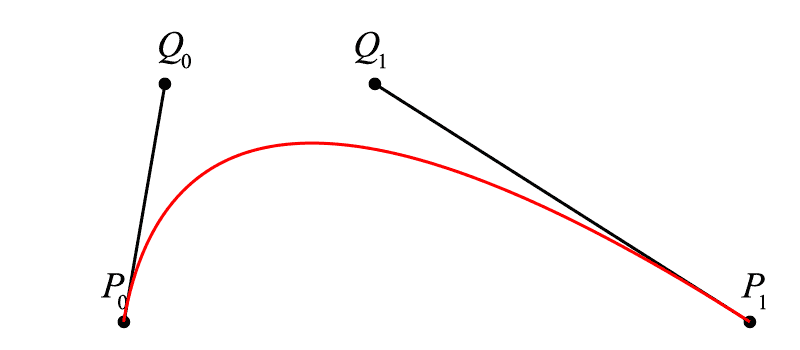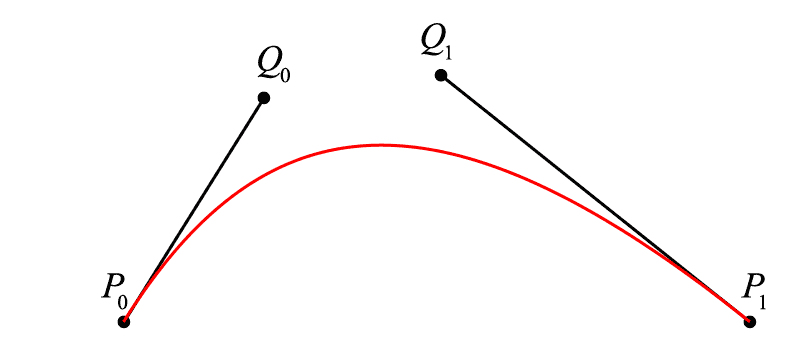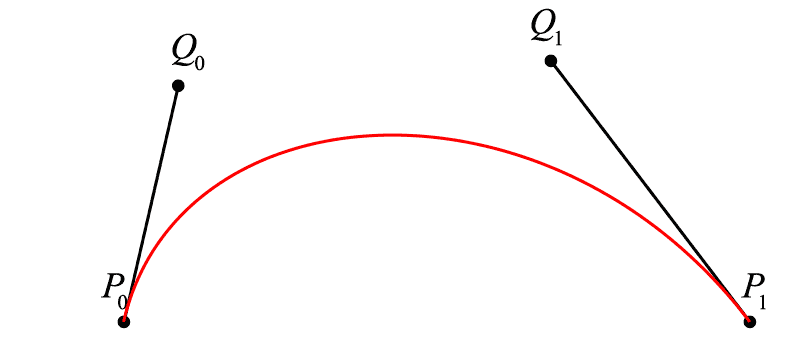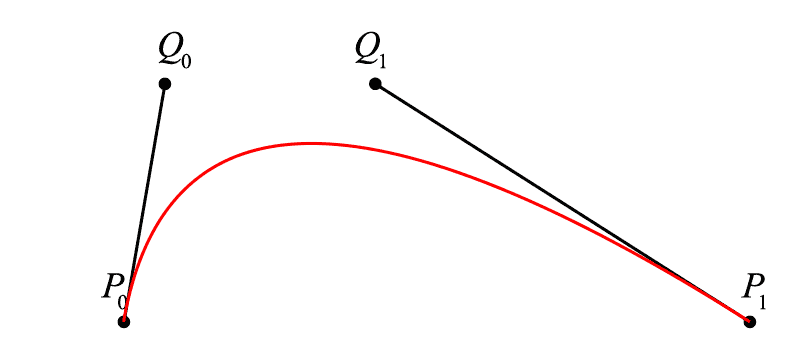
啊哈!现在我们终于找到这两个捣乱的黄色小球了,事实上在绝大多数的 GUI 工具界面中,如果用贝塞尔算法来描绘曲线,它们基本都是三次贝塞尔的方式,用四个点来决定一条曲线。
既然现在两个小球已经对我们来说已经是透明的了,那么我们何不算一算它们该呆在什么地方?
我们先来定义现在正在寻找的一类曲线为:<math><semantics><mrow><mi>y</mi><mo>=</mo><mi>n</mi><msup><mi>x</mi><mrow><mn>2</mn></mrow></msup></mrow><annotation encoding="application/x-tex">y=nx^{2}</annotation></semantics></math>y=nx2
结合上图,我们有如下表述:
<math><semantics><mrow><mrow><msub><mi>P</mi><mn>0</mn></msub></mrow><mo>=</mo><mrow><mo fence="true">(</mo><mrow><mtable><mtr><mtd><mrow><mn>0</mn></mrow></mtd><mtd><mrow><mn>0</mn></mrow></mtd></mtr></mtable></mrow><mo fence="true">)</mo></mrow><mo separator="true">,</mo><mrow><msub><mi>Q</mi><mn>0</mn></msub></mrow><mo>=</mo><mrow><mo fence="true">(</mo><mrow><mtable><mtr><mtd><mrow><mi>a</mi></mrow></mtd><mtd><mrow><mn>0</mn></mrow></mtd></mtr></mtable></mrow><mo fence="true">)</mo></mrow><mo separator="true">,</mo><mrow><msub><mi>Q</mi><mn>1</mn></msub></mrow><mo>=</mo><mrow><mo fence="true">(</mo><mrow><mtable><mtr><mtd><mrow><mi>b</mi></mrow></mtd><mtd><mrow><mi>c</mi></mrow></mtd></mtr></mtable></mrow><mo fence="true">)</mo></mrow><mo separator="true">,</mo><mrow><msub><mi>P</mi><mn>1</mn></msub></mrow><mo>=</mo><mrow><mo fence="true">(</mo><mrow><mtable><mtr><mtd><mrow><mi>x</mi></mrow></mtd><mtd><mrow><mrow><mi>n</mi><mrow><msup><mi>x</mi><mn>2</mn></msup></mrow></mrow></mrow></mtd></mtr></mtable></mrow><mo fence="true">)</mo></mrow></mrow><annotation encoding="application/x-tex">{P_0} = \left( {\begin{array}{l} 0&0 \end{array}} \right),{Q_0} = \left( {\begin{array}{l} a&0 \end{array}} \right),{Q_1} = \left( {\begin{array}{l} b&c \end{array}} \right),{P_1} = \left( {\begin{array}{l} x&{n{x^2}} \end{array}} \right)</annotation></semantics></math>P0=(00),Q0=(a0),Q1=(bc),P1=(xnx2)
<math><semantics><mrow><mrow><msub><mi>k</mi><mrow><mrow><msub><mi>P</mi><mn>0</mn></msub></mrow><mrow><msub><mi>Q</mi><mn>0</mn></msub></mrow></mrow></msub></mrow><mo>=</mo><mn>0</mn></mrow><annotation encoding="application/x-tex">{k_{{P_0}{Q_0}}} = 0</annotation></semantics></math>kP0Q0=0
<math><semantics><mrow><mrow><msub><mi>k</mi><mrow><mrow><msub><mi>P</mi><mn>1</mn></msub></mrow><mrow><msub><mi>Q</mi><mn>1</mn></msub></mrow></mrow></msub></mrow><mo>=</mo><mn>2</mn><mi>n</mi><mi>x</mi></mrow><annotation encoding="application/x-tex">{k_{{P_1}{Q_1}}} = 2nx</annotation></semantics></math>kP1Q1=2nx
其中 <math><semantics><mrow><mi>k</mi></mrow><annotation encoding="application/x-tex">k</annotation></semantics></math>k 为该切线的斜率(希望我们没有忘记前文讨论曲线的物理涵义时得到的结论),而我们需要求的就是 <math><semantics><mrow><mi>a</mi></mrow><annotation encoding="application/x-tex">a</annotation></semantics></math>a , <math><semantics><mrow><mi>b</mi></mrow><annotation encoding="application/x-tex">b</annotation></semantics></math>b , <math><semantics><mrow><mi>c</mi></mrow><annotation encoding="application/x-tex">c</annotation></semantics></math>c 三个值,那么我们结合三次贝塞尔方程,列式如下:
<math><semantics><mrow><mi>B</mi><mo>(</mo><mi>x</mi><mo>)</mo><mo>=</mo><mn>3</mn><mi>t</mi><mrow><mo>(</mo><mn>1</mn><mo>−</mo><mi>t</mi><msup><mo>)</mo><mn>2</mn></msup></mrow><mi>a</mi><mo>+</mo><mn>3</mn><mrow><msup><mi>t</mi><mn>2</mn></msup></mrow><mo>(</mo><mn>1</mn><mo>−</mo><mi>t</mi><mo>)</mo><mi>b</mi><mo>+</mo><mrow><msup><mi>t</mi><mn>3</mn></msup></mrow><mi>x</mi><mo>=</mo><mi>t</mi><mi>x</mi><mspace width="1em"></mspace></mrow><annotation encoding="application/x-tex">B(x) = 3t{(1 - t)^2}a + 3{t^2}(1 - t)b + {t^3}x = tx \quad</annotation></semantics></math>B(x)=3t(1−t)2a+3t2(1−t)b+t3x=tx ①
<math><semantics><mrow><mi>B</mi><mo>(</mo><mi>y</mi><mo>)</mo><mo>=</mo><mn>3</mn><mrow><msup><mi>t</mi><mn>2</mn></msup></mrow><mo>(</mo><mn>1</mn><mo>−</mo><mi>t</mi><mo>)</mo><mi>c</mi><mo>+</mo><mi>n</mi><mrow><msup><mi>t</mi><mn>3</mn></msup></mrow><mrow><msup><mi>x</mi><mn>2</mn></msup></mrow><mo>=</mo><mi>n</mi><mrow><msup><mi>t</mi><mn>2</mn></msup></mrow><mrow><msup><mi>x</mi><mn>2</mn></msup></mrow></mrow><annotation encoding="application/x-tex">B(y) = 3{t^2}(1 - t)c + n{t^3}{x^2} = n{t^2}{x^2}</annotation></semantics></math>B(y)=3t2(1−t)c+nt3x2=nt2x2 ②
注意到,②式只含有一个变量 c ,因此我们从它入手化简如下:
<math><semantics><mrow><mtable><mtr><mtd><mrow><mi>B</mi><mo>(</mo><mi>y</mi><mo>)</mo><mo>=</mo><mn>3</mn><mrow><msup><mi>t</mi><mn>2</mn></msup></mrow><mo>(</mo><mn>1</mn><mo>−</mo><mi>t</mi><mo>)</mo><mi>c</mi><mo>+</mo><mi>n</mi><mrow><msup><mi>t</mi><mn>3</mn></msup></mrow><mrow><msup><mi>x</mi><mn>2</mn></msup></mrow><mo>=</mo><mi>n</mi><mrow><msup><mi>t</mi><mn>2</mn></msup></mrow><mrow><msup><mi>x</mi><mn>2</mn></msup></mrow></mrow></mtd></mtr><mtr><mtd><mrow><mspace width="1em"></mspace><mspace width="1em"></mspace><mo>⇒</mo><mn>3</mn><mi>c</mi><mo>⋅</mo><mo>(</mo><mrow><msup><mi>t</mi><mn>3</mn></msup></mrow><mo>−</mo><mrow><msup><mi>t</mi><mn>2</mn></msup></mrow><mo>)</mo><mo>=</mo><mi>n</mi><mrow><msup><mi>x</mi><mn>2</mn></msup></mrow><mo>(</mo><mrow><msup><mi>t</mi><mn>3</mn></msup></mrow><mo>−</mo><mrow><msup><mi>t</mi><mn>2</mn></msup></mrow><mo>)</mo></mrow></mtd></mtr></mtable></mrow><annotation encoding="application/x-tex">\begin{array}{l} B(y) = 3{t^2}(1 - t)c + n{t^3}{x^2} = n{t^2}{x^2}\\ \quad \quad \Rightarrow 3c \cdot ({t^3} - {t^2}) = n{x^2}({t^3} - {t^2}) \end{array}</annotation></semantics></math>B(y)=3t2(1−t)c+nt3x2=nt2x2⇒3c⋅(t3−t2)=nx2(t3−t2)
显然,当 <math><semantics><mrow><msup><mi>t</mi><mn>3</mn></msup><mo>−</mo><msup><mi>t</mi><mn>2</mn></msup></mrow><annotation encoding="application/x-tex">t^3-t^2</annotation></semantics></math>t3−t2 为 <math><semantics><mrow><mn>0</mn></mrow><annotation encoding="application/x-tex">0</annotation></semantics></math>0 时,就是到达了这个曲线的起点和终点,因此我们只需令 <math><semantics><mrow><msup><mi>t</mi><mn>3</mn></msup><mo>−</mo><msup><mi>t</mi><mn>2</mn></msup></mrow><annotation encoding="application/x-tex">t^3-t^2</annotation></semantics></math>t3−t2 不为零,即可求出:
<math><semantics><mrow><mn>3</mn><mi>c</mi><mo>=</mo><mi>n</mi><msup><mi>x</mi><mrow><mn>2</mn></mrow></msup></mrow><annotation encoding="application/x-tex">3c=nx^{2}</annotation></semantics></math>3c=nx2
<math><semantics><mrow><mi>c</mi><mo>=</mo><mfrac><mrow><mi>n</mi><msup><mi>x</mi><mrow><mn>2</mn></mrow></msup></mrow><mrow><mn>3</mn></mrow></mfrac><mo>=</mo><mfrac><mrow><mi>y</mi></mrow><mrow><mn>3</mn></mrow></mfrac><mspace width="1em"></mspace><mspace width="1em"></mspace></mrow><annotation encoding="application/x-tex">c=\frac{nx^{2}}{3}=\frac{y}{3} \quad \quad</annotation></semantics></math>c=3nx2=3y ③
又,我们可以直接以 <math><semantics><mrow><msub><mi>P</mi><mrow><mn>1</mn></mrow></msub><mo separator="true">,</mo><msub><mi>Q</mi><mrow><mn>1</mn></mrow></msub></mrow><annotation encoding="application/x-tex">P_{1},Q_{1}</annotation></semantics></math>P1,Q1 的坐标来表示其斜率:
<math><semantics><mrow><mrow><msub><mi>k</mi><mrow><mrow><msub><mi>P</mi><mn>1</mn></msub></mrow><mrow><msub><mi>Q</mi><mn>1</mn></msub></mrow></mrow></msub></mrow><mo>=</mo><mn>2</mn><mi>n</mi><mi>x</mi><mo>=</mo><mfrac><mrow><mrow><mi>n</mi><mrow><msup><mi>x</mi><mn>2</mn></msup></mrow><mo>−</mo><mi>c</mi></mrow></mrow><mrow><mrow><mi>x</mi><mo>−</mo><mi>b</mi></mrow></mrow></mfrac></mrow><annotation encoding="application/x-tex">{k_{{P_1}{Q_1}}} = 2nx = \frac{{n{x^2} - c}}{{x - b}}</annotation></semantics></math>kP1Q1=2nx=x−bnx2−c
将③代入其中可得:
<math><semantics><mrow><mtable><mtr><mtd><mrow><mn>2</mn><mi>n</mi><mi>x</mi><mo>(</mo><mi>x</mi><mo>−</mo><mi>b</mi><mo>)</mo><mo>=</mo><mfrac><mrow><mn>2</mn></mrow><mrow><mn>3</mn></mrow></mfrac><mi>n</mi><mrow><msup><mi>x</mi><mn>2</mn></msup></mrow></mrow></mtd></mtr><mtr><mtd><mrow><mspace width="1em"></mspace><mo>⇒</mo><mi>x</mi><mo>−</mo><mi>b</mi><mo>=</mo><mfrac><mrow><mi>x</mi></mrow><mrow><mn>3</mn></mrow></mfrac></mrow></mtd></mtr></mtable></mrow><annotation encoding="application/x-tex">\begin{array}{l} 2nx(x - b) = \frac{2}{3}n{x^2}\\ \quad \Rightarrow x - b = \frac{x}{3} \end{array}</annotation></semantics></math>2nx(x−b)=32nx2⇒x−b=3x
<math><semantics><mrow><mi>b</mi><mo>=</mo><mfrac><mrow><mn>2</mn></mrow><mrow><mn>3</mn></mrow></mfrac><mi>x</mi><mspace width="1em"></mspace><mspace width="1em"></mspace><mspace width="1em"></mspace></mrow><annotation encoding="application/x-tex">b = \frac{2}{3}x\quad\quad\quad</annotation></semantics></math>b=32x ④
再将④代入①式可求得 a 如下:
<math><semantics><mrow><mtable><mtr><mtd><mrow><mi>B</mi><mo>(</mo><mi>x</mi><mo>)</mo><mo>=</mo><mn>3</mn><mi>t</mi><mrow><mo>(</mo><mn>1</mn><mo>−</mo><mi>t</mi><msup><mo>)</mo><mn>2</mn></msup></mrow><mi>a</mi><mo>+</mo><mn>2</mn><mrow><msup><mi>t</mi><mn>2</mn></msup></mrow><mo>(</mo><mn>1</mn><mo>−</mo><mi>t</mi><mo>)</mo><mi>x</mi><mo>+</mo><mrow><msup><mi>t</mi><mn>3</mn></msup></mrow><mi>x</mi><mo>=</mo><mi>t</mi><mi>x</mi></mrow></mtd></mtr><mtr><mtd><mrow><mspace width="1em"></mspace><mspace width="1em"></mspace><mtext> </mtext><mo>⇒</mo><mn>3</mn><mi>a</mi><mo>⋅</mo><mo>(</mo><mrow><msup><mi>t</mi><mn>3</mn></msup></mrow><mo>−</mo><mn>2</mn><mrow><msup><mi>t</mi><mn>2</mn></msup></mrow><mo>+</mo><mn>1</mn><mo>)</mo><mo>=</mo><mi>x</mi><mo>⋅</mo><mo>(</mo><mrow><msup><mi>t</mi><mn>3</mn></msup></mrow><mo>−</mo><mn>2</mn><mrow><msup><mi>t</mi><mn>2</mn></msup></mrow><mo>+</mo><mn>1</mn><mo>)</mo></mrow></mtd></mtr></mtable></mrow><annotation encoding="application/x-tex">\begin{array}{l} B(x) = 3t{(1 - t)^2}a + 2{t^2}(1 - t)x + {t^3}x = tx\\ \quad \quad \ \Rightarrow 3a \cdot ({t^3} - 2{t^2} + 1) = x \cdot ({t^3} - 2{t^2} + 1) \end{array}</annotation></semantics></math>B(x)=3t(1−t)2a+2t2(1−t)x+t3x=tx ⇒3a⋅(t3−2t2+1)=x⋅(t3−2t2+1)
<math><semantics><mrow><mi>a</mi><mo>=</mo><mfrac><mrow><mi>x</mi></mrow><mrow><mn>3</mn></mrow></mfrac></mrow><annotation encoding="application/x-tex">a = \frac{x}{3}</annotation></semantics></math>a=3x
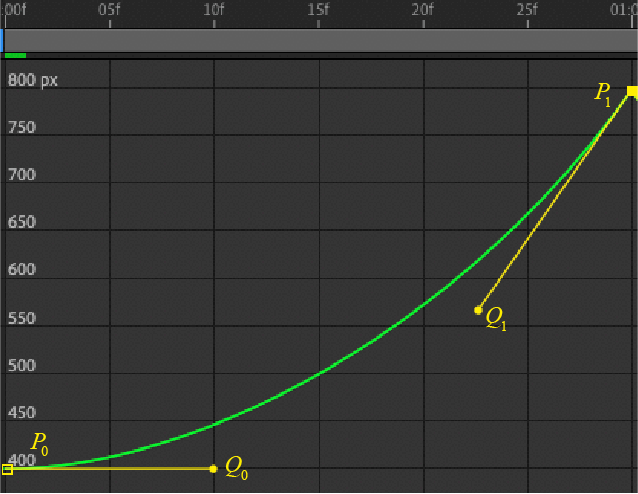
至此,我们得到了当我们的曲线为 <math><semantics><mrow><mi>y</mi><mo>=</mo><mi>n</mi><msup><mi>x</mi><mn>2</mn></msup></mrow><annotation encoding="application/x-tex">y=nx^2</annotation></semantics></math>y=nx2 时,用来描绘它的三次贝塞尔需要的所有四个点的坐标:
<math><semantics><mrow><mrow><msub><mi>P</mi><mn>0</mn></msub></mrow><mo>=</mo><mrow><mo fence="true">(</mo><mrow><mtable><mtr><mtd><mrow><mn>0</mn></mrow></mtd><mtd><mrow><mn>0</mn></mrow></mtd></mtr></mtable></mrow><mo fence="true">)</mo></mrow><mo separator="true">,</mo><mrow><msub><mi>Q</mi><mn>0</mn></msub></mrow><mo>=</mo><mrow><mo fence="true">(</mo><mrow><mtable><mtr><mtd><mrow><mrow><mfrac><mrow><mi>x</mi></mrow><mrow><mn>3</mn></mrow></mfrac></mrow></mrow></mtd><mtd><mrow><mn>0</mn></mrow></mtd></mtr></mtable></mrow><mo fence="true">)</mo></mrow><mo separator="true">,</mo><mrow><msub><mi>Q</mi><mn>1</mn></msub></mrow><mo>=</mo><mrow><mo fence="true">(</mo><mrow><mtable><mtr><mtd><mrow><mrow><mfrac><mrow><mrow><mn>2</mn><mi>x</mi></mrow></mrow><mrow><mn>3</mn></mrow></mfrac></mrow></mrow></mtd><mtd><mrow><mrow><mfrac><mrow><mi>y</mi></mrow><mrow><mn>3</mn></mrow></mfrac></mrow></mrow></mtd></mtr></mtable></mrow><mo fence="true">)</mo></mrow><mo separator="true">,</mo><mrow><msub><mi>P</mi><mn>1</mn></msub></mrow><mo>=</mo><mrow><mo fence="true">(</mo><mrow><mtable><mtr><mtd><mrow><mi>x</mi></mrow></mtd><mtd><mrow><mi>y</mi></mrow></mtd></mtr></mtable></mrow><mo fence="true">)</mo></mrow></mrow><annotation encoding="application/x-tex">{P_0} = \left( {\begin{array}{l} 0&0 \end{array}} \right),{Q_0} = \left( {\begin{array}{l} {\frac{x}{3}}&0 \end{array}} \right),{Q_1} = \left( {\begin{array}{l} {\frac{{2x}}{3}}&{\frac{y}{3}} \end{array}} \right),{P_1} = \left( {\begin{array}{l} x&y \end{array}} \right)</annotation></semantics></math>P0=(00),Q0=(3x0),Q1=(32x3y),P1=(xy)
对于我们前文建立的运动图像来说,只需要简单换一下单位: <math><semantics><mrow><mi>x</mi><mo>→</mo><mi>t</mi><mo separator="true">,</mo><mtext> </mtext><mtext> </mtext><mi>y</mi><mo>→</mo><mi>s</mi></mrow><annotation encoding="application/x-tex">x\rightarrow t,\ \ y\rightarrow s</annotation></semantics></math>x→t, y→s ,如此我们就知道应该编辑曲线如下图:
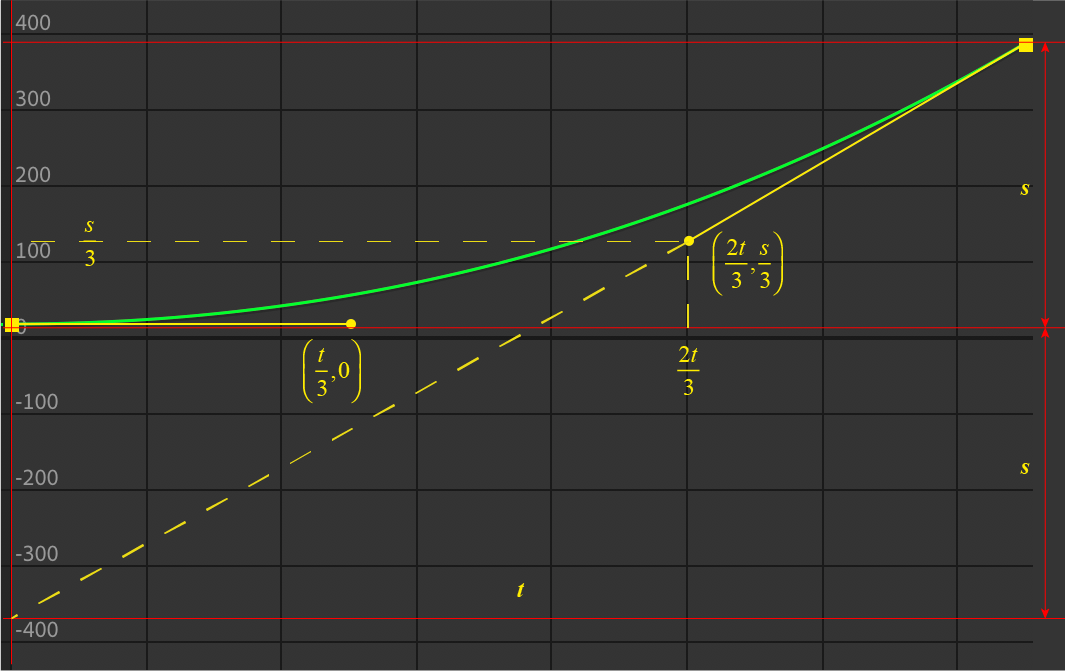
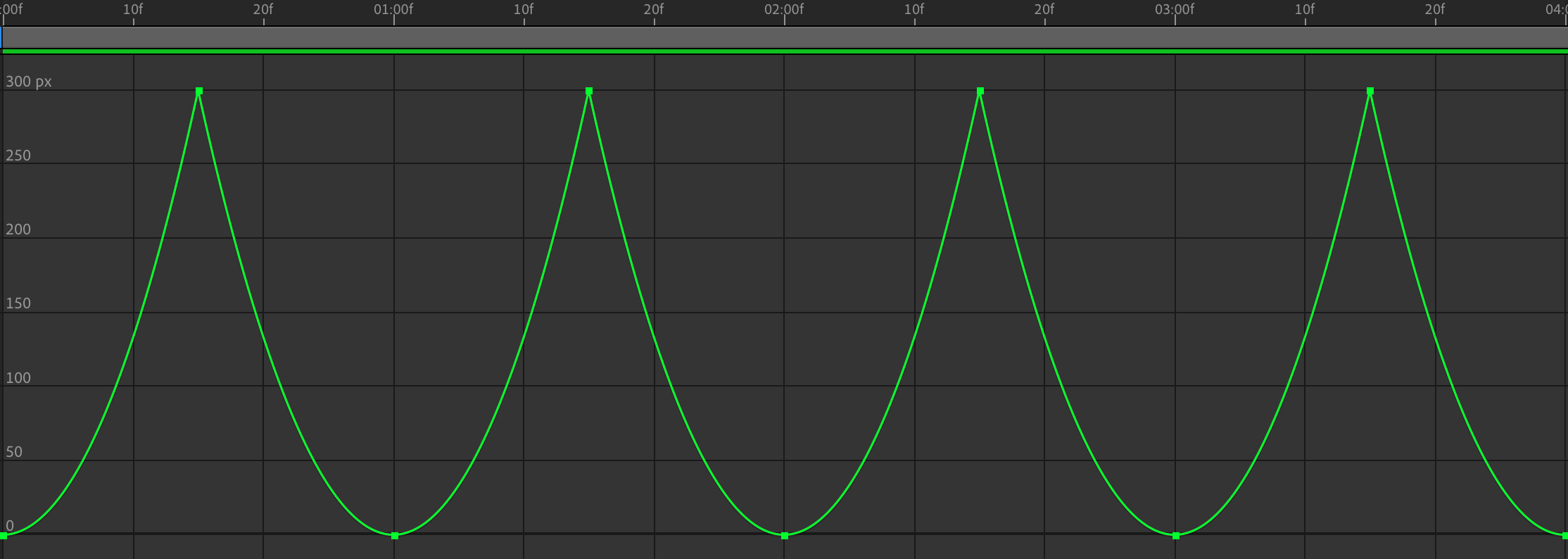
终于!我们得到了这个简单的答案,没有谁会怀疑这个答案的简单明了,但是很少有人知道这种简单背后蕴含了多少努力和多么美妙而强大的力量,我们自己对这种努力和力量的认识又处在哪种高度呢?这是一个值得时时刻刻扪心自问的终极问题。
7. 一个终究会停止弹跳的小球
现在我们的小球可以永无休止地往复弹跳了,它的图像显示如下:
我们还可以通过更改坐标轴来检查这是不是一个匀加速运动
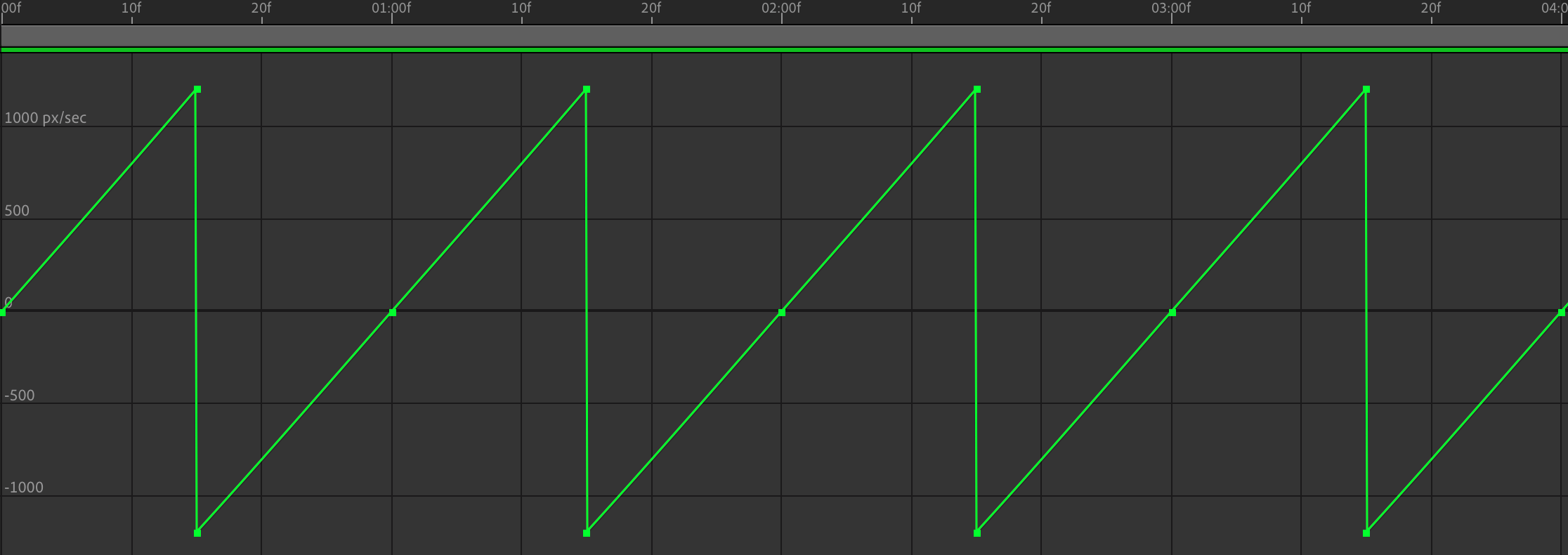
如图,我们将纵轴改为速度,很显然它是完美的直线,同时我们可以通过查看点的具体数值,来验算是否足够精确,其正负的瞬间切换改变代表的是落地后方向的转换,而加速度,也就是其斜率从未改变。真是完美的匀加速运动!我们真是棒棒哒小天才(并不)。
但是,有一个问题,如果这是真实自然的坠落弹跳,那它一定是会停下来的,怎么能够让它符合自然直觉地停下呢?我们似乎只要让每次弹跳的高度降低一些,相应地时间也缩短一些,就可以了?我们不妨将每次的波形等比缩放试试。
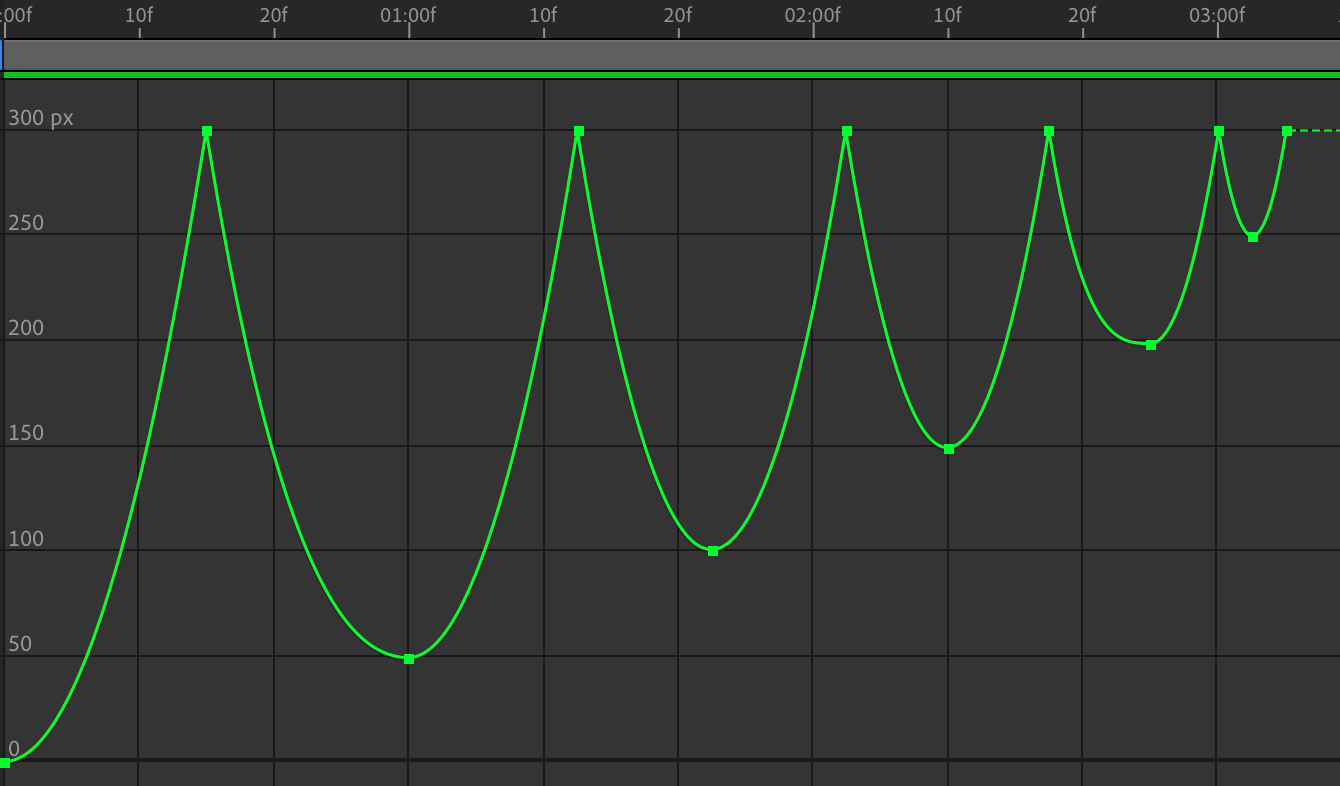
显然,运行一下就知道,这是大错特错的。我们敏锐地意识到: <math><semantics><mrow><mi>s</mi><mo>=</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac><mi>a</mi><msup><mi>t</mi><mrow><mn>2</mn></mrow></msup></mrow><annotation encoding="application/x-tex">s=\frac{1}{2}at^{2}</annotation></semantics></math>s=21at2,位移和时间有一个二次的而非线性的比例关系。但是我们费了很大功夫才能刚刚模仿好一个二次的曲线而已,现在如果再让我们模拟二次的缩放比例关系岂不是……不过不要紧,我们有小天才一般的数学直觉:一个二次函数的导数是线性的。
当然,这是一个物理问题,我们希望物理地去看待。在处理碰撞这一类问题中,我们显然会用到动量守恒和能量守恒(最后一节我们会来讨论这两种守恒的由来和意义所在)。在这个例子中,我们并不需要为小球和地面构建成一个系统,所以我们基于能量守恒可以列式如下:
<math><semantics><mrow><mi>e</mi><mfrac><mrow><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac><mi>m</mi><msubsup><mi>v</mi><mrow><mn>0</mn></mrow><mrow><mn>2</mn></mrow></msubsup><mo>=</mo><mfrac><mrow><mn>1</mn></mrow><mrow><mn>2</mn></mrow></mfrac><mi>m</mi><msubsup><mi>v</mi><mrow><mn>1</mn></mrow><mrow><mn>2</mn></mrow></msubsup></mrow><annotation encoding="application/x-tex">e\frac{1}{2}mv_{0}^{2}=\frac{1}{2}mv_{1}^{2}</annotation></semantics></math>e21mv02=21mv12
其中 <math><semantics><mrow><msub><mi>v</mi><mrow><mn>0</mn></mrow></msub></mrow><annotation encoding="application/x-tex">v_{0}</annotation></semantics></math>v0 是小球落地时的速度, <math><semantics><mrow><msub><mi>v</mi><mrow><mn>1</mn></mrow></msub></mrow><annotation encoding="application/x-tex">v_{1}</annotation></semantics></math>v1 是小球回弹的速度,e是能量留存的比例,我们不难发现,当 <math><semantics><mrow><mi>e</mi><mo>=</mo><mn>1</mn></mrow><annotation encoding="application/x-tex">e=1</annotation></semantics></math>e=1 时,对应的是小球无限弹跳,即完全弹性碰撞;当 <math><semantics><mrow><mi>e</mi><mo>=</mo><mn>0</mn></mrow><annotation encoding="application/x-tex">e=0</annotation></semantics></math>e=0 时,对应的是小球触地即停,即完全非弹性碰撞;而我们要处理的是非完全弹性碰撞,即 <math><semantics><mrow><mn>0</mn><mo><</mo><mi>e</mi><mo><</mo><mn>1</mn></mrow><annotation encoding="application/x-tex">0<e<1</annotation></semantics></math>0<e<1 时。则我们有:
<math><semantics><mrow><msqrt><mrow><mi>e</mi></mrow></msqrt><msub><mi>v</mi><mrow><mn>0</mn></mrow></msub><mo>=</mo><msub><mi>v</mi><mrow><mn>1</mn></mrow></msub></mrow><annotation encoding="application/x-tex">\sqrt{e}v_{0}=v_{1}</annotation></semantics></math>√ev0=v1
我们借助这个弹跳函数的基本表达式,可以得到如下的的比例关系:
<math><semantics><mrow><mi>e</mi><msub><mi>s</mi><mrow><mn>0</mn></mrow></msub><mo>=</mo><msub><mi>s</mi><mrow><mn>1</mn></mrow></msub></mrow><annotation encoding="application/x-tex">es_{0}=s_{1}</annotation></semantics></math>es0=s1
<math><semantics><mrow><msqrt><mrow><mi>e</mi></mrow></msqrt><msub><mi>t</mi><mrow><mn>0</mn></mrow></msub><mo>=</mo><msub><mi>t</mi><mrow><mn>1</mn></mrow></msub></mrow><annotation encoding="application/x-tex">\sqrt{e}t_{0}=t_{1}</annotation></semantics></math>√et0=t1
果然,我们看出来,位移缩短的比例和时间缩短的比例是不同的,位移在以 <math><semantics><mrow><mi>e</mi></mrow><annotation encoding="application/x-tex">e</annotation></semantics></math>e 为倍数缩放,而时间在以 <math><semantics><mrow><msqrt><mrow><mi>e</mi></mrow></msqrt></mrow><annotation encoding="application/x-tex">\sqrt{e}</annotation></semantics></math>√e 为倍数缩放,我们在前文中,等比缩放位移/时间图像的错误就在于这里。所以,这就是我们小天才般的数学直觉的本质:速度/时间图像才是我们应该等比缩放的!我们转向本节最开始用来检查的速度/时间图像,作出如下缩放:

弹跳完美地渐停了!我们注意到,这种速度/时间函数的等比缩放其实质就是:改变的回弹速度,不变的斜率——加速度。这也就是这类碰撞所没有改变的本质属性:能量有所损失,但是这仍是匀加速运动。
当然,以 AE 为例,我们发现在操作速度图像时,无法改变小球回弹的高度,最终我们能够操作的也只有时间和位移这两种属性而已。那么如何来构造出上图这样等比缩放的效果呢?
不精确的办法是先编辑速度/时间图像,来保证两点:1. 保证速度按比例减少;2. 保证时间和速度比值一致——即每一次弹起下落的三点间斜率一致——加速度不变。然后,再回到位移/时间图像中,调整每次弹起的高度,使速度/时间图像每三点之间的曲线连成直线。
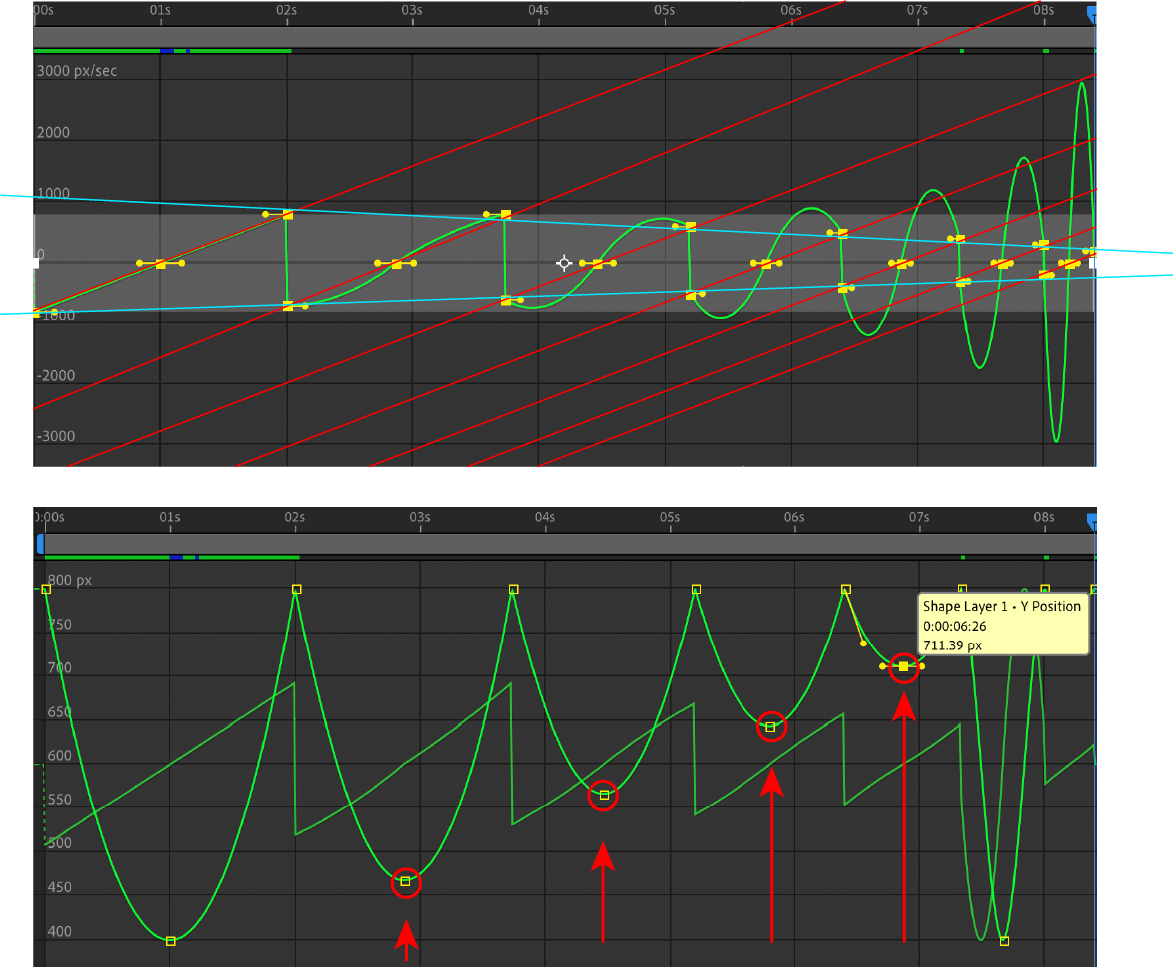
当然,我们可能喜欢精确的手法:
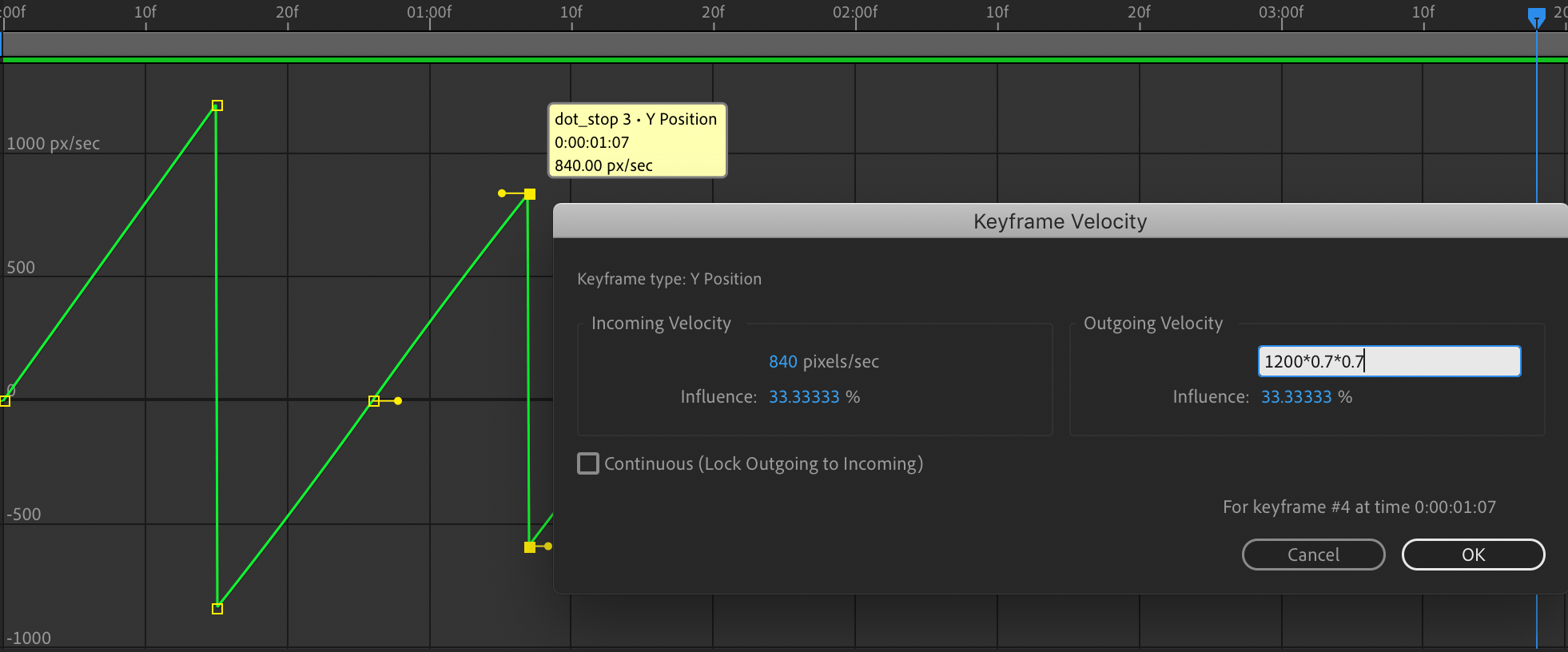
具体的操作根据不同软件的功能和我们自己看待一个运动学函数的不同角度而都会有所区别,只要我们追本溯源,在数学和物理上获取其本质的关系,都会指引我们走向唯一正确的模拟。
最后,我们希望自己不要忘记,我们无法凭借手动来严格拟合本文中推导的各类关系,在大多数时间,我们也并不需要如此拟真的效果,甚至会为了夸张等效果作出反常识的动态效果。
它们的作用,也就是这篇文章真正的意义,在于:我们如此设置运动的曲线,不是因为我们“感觉”这样做会“自然”一些,而是因为我们知道,“自然”的运动是被如此描述并图像化表达的,所以我们应该去这么做。
8. 见山是山
未完待续


