写在前面
上回书说到一个新的代价函数,今次我们就来简单的介绍一下它,这将成为我们的新武器。
代价函数
为什么我们不使用之前的均方差代价函数呢是因为逻辑回归模型沿用均方差得到的代价函数将是一个非凸函数,而非凸函数十分样貌十分的扭曲,一点都不丝滑,这将导致梯度下降遭遇局部最优问题。
还记得我们之前在线性回归的梯度下降吗?可以形象的理解成怎么才能最快速的从山顶跳下去,而局部最优则是在坑坑洼洼的山上,你以为你已经跳崖成功了,其实这是自缘身在此山中,你依然在半山腰。
为解决这个问题,我们需要重新定义逻辑回归的代价函数,凸优化J(θ)
这样构建的Cost(hθ(x),y)函数的特点:
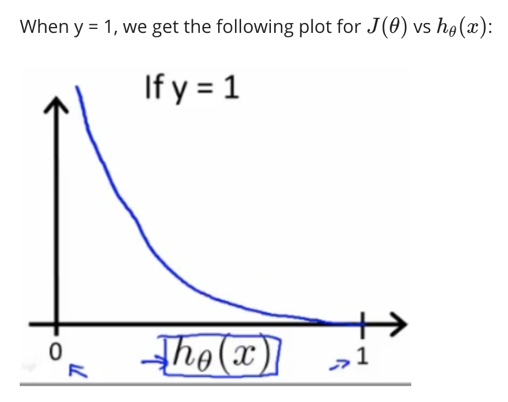
当实际的y=1且hθ也为1时误差为0,当y=1但hθ不为1时误差随着hθ的变小而变大
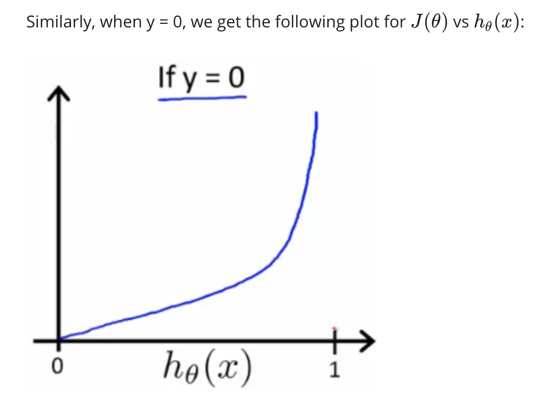
当实际的y=0且hθ也为0时代价为0,当y=0但hθ不为0时误差随着hθ的变大而变大
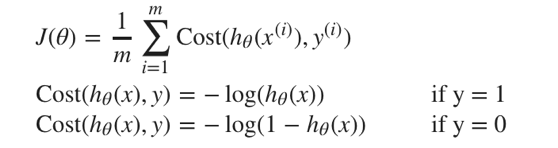
逻辑回归的代价函数
我们的目的是让以下的函数损失最小
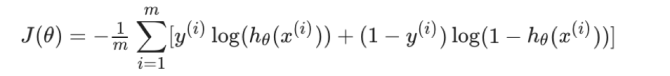
与线性回归一样,不停的更新theta
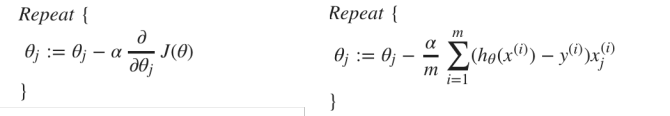
小注意点:

写在后面
到目前为止,对于机器学习线性回归和逻辑回归的简单介绍就差不多了。由于涉及到一些简单的数学推导,下一次将简单分享一下一些有关于求导的数学知识,respect!
